 por Thiago 86 » Qua Mar 06, 2013 22:39
por Thiago 86 » Qua Mar 06, 2013 22:39
Saudações!
Estou resolvendo um problema mas as letras: A e B não estão deichando eu sair do canto. O problema é:
Os valores de A e B , que satisfazem a igualdade
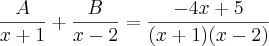
são raizes da equação:
Não sei como tirá o m.m.c dessas frações.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 00:15
por Russman » Qui Mar 07, 2013 00:15
Não se preocupe com o m.m.c ... ele é bom? Sim, mas não estritamente necessário. Se você proceder da seguinte forma
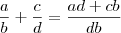
o máximo que terá, talvez, de fazer é simplificar o resultado.
Assim, para somar
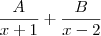
basta fazer a multiplicação
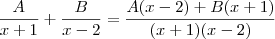
.
Como
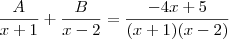
então
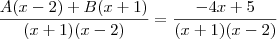
,
e simplificando os denominadores em ambos membros da equação, temos
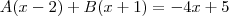
de onde, por igualdade de polinômios,
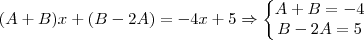
Agora basta resolver o sistema. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qui Mar 07, 2013 08:21
por Thiago 86 » Qui Mar 07, 2013 08:21
Saldações

! Valeu por responder minha duvida. Mas bateu outra, a formula
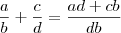
eu tenho que decorá? E em quais ocasiões eu devo usar?
E qual foi o caminho que você usou para sair daqui
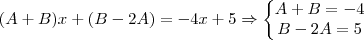
e chegar aqui?
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 08:46
por Russman » Qui Mar 07, 2013 08:46
Thiago 86 escreveu:Saldações ! Valeu por responder minha duvida. Mas bateu outra, a formula eu tenho que decorá? E em quais ocasiões eu devo usar?
Essa fórmula é a que usamos para somar frações! Decorá-la será uma consequência de usá-la seguidamente.
Thiago 86 escreveu:E qual foi o caminho que você usou para sair daqui e chegar aqui?
Igualdade de polinômios. Se um polinômio

é identicamente igual a outro

, isto é,

para qualquer valor de

( e não alguns em particular) então os coeficientes de

são iguais aos de

.
Você tem dois polinômios de 1° grau que DEVEM ser iguai. Assim, o coeficiente de

do lado esquerdo tem de ser igual ao do lado direito e o termo independente( aquele que não tem

o multiplicando) também.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qui Mar 07, 2013 18:54
por Thiago 86 » Qui Mar 07, 2013 18:54
Agradecido.

-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
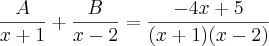 são raizes da equação:
são raizes da equação:
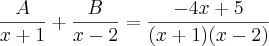 são raizes da equação:
são raizes da equação:
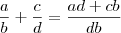
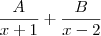
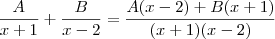 .
.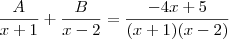
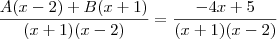 ,
,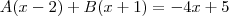
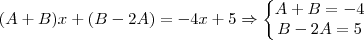

 ! Valeu por responder minha duvida. Mas bateu outra, a formula
! Valeu por responder minha duvida. Mas bateu outra, a formula 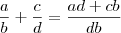 eu tenho que decorá? E em quais ocasiões eu devo usar?
eu tenho que decorá? E em quais ocasiões eu devo usar?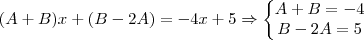 e chegar aqui?
e chegar aqui?
 é identicamente igual a outro
é identicamente igual a outro  , isto é,
, isto é,  para qualquer valor de
para qualquer valor de  ( e não alguns em particular) então os coeficientes de
( e não alguns em particular) então os coeficientes de  são iguais aos de
são iguais aos de  .
. do lado esquerdo tem de ser igual ao do lado direito e o termo independente( aquele que não tem
do lado esquerdo tem de ser igual ao do lado direito e o termo independente( aquele que não tem  o multiplicando) também.
o multiplicando) também.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.