 por klueger » Sáb Mar 02, 2013 18:52
por klueger » Sáb Mar 02, 2013 18:52
Seja a função:
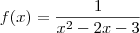
Usando o método das
Frações Parciais, calcule sua área, sendo, para isto, a sua
integral:
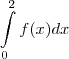
Estou sem noção de Frações, já consultei tabela e não achei...
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Dom Mar 03, 2013 19:41
por Russman » Dom Mar 03, 2013 19:41
Primeiramente, você precisa decompor o polinômio do denominador em fatores. Como ele é de segundo grau sabemos que é possível escrever

onde

e

são as raízes desse polinômio. Claramente podemos tomar

e

. Assim,
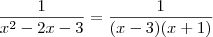
.
Agora suponha a existência de dois valores reais

e

tais que

.
Desenvolvendo,
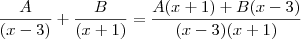
e por igualdade de polinômios, temos

Assim,
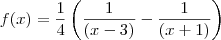
.
Agora é só integrar lembrando que
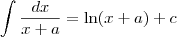
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizAquino » Ter Mar 05, 2013 10:19
por LuizAquino » Ter Mar 05, 2013 10:19
klueger escreveu:Seja a função:
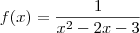
Usando o método das
Frações Parciais, calcule sua área, sendo, para isto, a sua
integral:
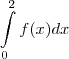
Estou sem noção de Frações, já consultei tabela e não achei...
Para revisar a técnica de Frações Parciais, eu gostaria de sugerir que você assista as videoaulas "29. Cálculo I - Integração por Frações Parciais (Caso I e II)" e "30. Cálculo I - Integração por Frações Parciais (Caso III e IV)". Essas videoaulas estão disponíveis no meu canal no YouTube:
http://www.youtube.com/LCMAquinoEu espero que essas videoaulas possam ajudar você no entendimento desta técnica.
Russman escreveu:Agora é só integrar lembrando que
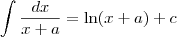
.
Apenas uma observação: o que temos na verdade seria

.
Em outras palavras, devemos ter o módulo em x + a.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Frações parciais.
por 380625 » Sex Jul 05, 2013 15:18
- 5 Respostas
- 3137 Exibições
- Última mensagem por young_jedi

Sáb Jul 13, 2013 10:41
Álgebra Elementar
-
- frações parciais
por fasaatyro » Qui Dez 04, 2014 09:18
- 1 Respostas
- 1145 Exibições
- Última mensagem por lucas_carvalho

Qui Dez 04, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Frações Parciais
por Bruhh » Qua Set 29, 2010 18:20
- 2 Respostas
- 5396 Exibições
- Última mensagem por Bruhh

Qui Set 30, 2010 08:40
Cálculo: Limites, Derivadas e Integrais
-
- [integral] fraçoes parciais
por ewald » Qui Set 08, 2011 15:10
- 1 Respostas
- 2112 Exibições
- Última mensagem por Neperiano

Qui Set 08, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- integrais por frações parciais
 por engrangel » Qua Abr 18, 2012 15:46
por engrangel » Qua Abr 18, 2012 15:46
- 2 Respostas
- 2934 Exibições
- Última mensagem por engrangel

Qui Abr 19, 2012 17:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
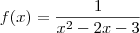
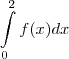

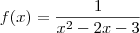
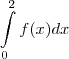


 e
e  são as raízes desse polinômio. Claramente podemos tomar
são as raízes desse polinômio. Claramente podemos tomar  e
e  . Assim,
. Assim,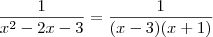 .
. e
e  tais que
tais que .
.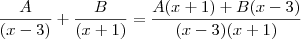

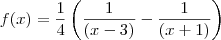 .
.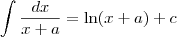 .
.
.
 .
.