Estou com um problema na seguinte questão:
Considere a função

1. Ache a equação da reta tangente ao gráfico de f(x) quando
 ;
;2. Calcule a área da região limitada por
 , a reta tangente encontrada no item anterior e o eixo x.
, a reta tangente encontrada no item anterior e o eixo x.------
O item 1 eu resolvi facilmente, pois a definição da reta tangente é
 , onde m é a inclinação da reta tangente (derivada da função).
, onde m é a inclinação da reta tangente (derivada da função).E quando
 a derivada de f é
a derivada de f é 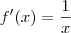
Então a reta tangente é
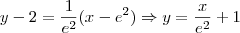
O problema é calcular a área... Não consigo nem imaginar como e onde a curva, a reta e o eixo x se interceptam... Se fosse só a reta e a curva, acho que seria mais fácil... De qualquer forma, quais seriam o intervalos de integração? Se alguém conseguir uma resolução detalhada, eu agradeço.



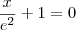



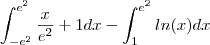

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.