MarlonMO250 escreveu:russman, essa definição que você falou eu conheço, o problema é que a professora pediu na lista usando essa que eu falei

felipeek, no caso a derivada não ficaria 2x+1, sendo que é 4x-3

Você está fazendo confusão.
A derivada da função que você deu é sim 4x-3.
Note, entretanto, que você tentou resolver o exercício tomando
p=2. No momento que você faz isso, você substitui todas as variáveis
p da definição por 2 e
x que tendia a
p passa a tender a 2 (esse último você esqueceu de modificar ali no limite). O fato de você escolher um valor para a variável
p faz você obter como o resultado não uma Função Derivada geral (que seria 4x-3) e sim o RESULTADO da derivada no ponto que você escolheu (no caso p=2). Se você quisesse obter como resultado 4x-3, você deveria ter calculado o limite sem assumir um valor para
p. Aí sim, o resultado seria uma função derivada geral 4x-3 (no caso seria 4p-3) e aí sim você poderia substituir o x por 2 na função, obtendo a derivada no ponto x=2 que seria 5 (4*2-3 = 5).
O meu cálculo deu 2x+1 como resultado porque eu não terminei. Como
x tendia a
2, o passo final seria substiuir o
x por
2, obtendo como reposta final: 2(2)+1 = 5 . Ou seja, cinco é a derivada de x=2, ou ainda, 5 é a inclinação da reta tangente quando x=2. Obtemos direto o resultado de 5, sem obter a função derivada primeiro, pois assumimos direto p=2 no começo do exercicio (pensei que era assim que vc queria, pois foi vc mesmo que fez assim, na verdade, talvez seja isso mesmo que o exercicio quer)


 , e p=2
, e p=2

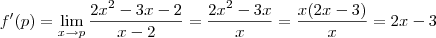

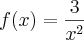 , e p=1
, e p=1![f(x)=\sqrt[3]{x} f(x)=\sqrt[3]{x}](/latexrender/pictures/415c4f39a1a68ccac15da99969baacfc.png) , e p=8
, e p=8


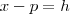 então teremos uma definição expressa de forma mais simples que, certamente o ajudará.
então teremos uma definição expressa de forma mais simples que, certamente o ajudará. .
.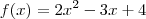 , então
, então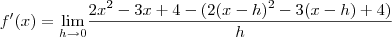
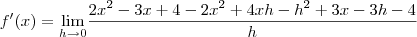
 .
. o limite se torna
o limite se torna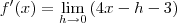 ,
, :
:
 :
: 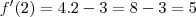

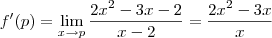
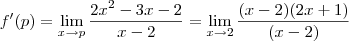



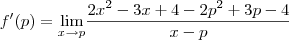
![f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ] f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ]](/latexrender/pictures/ccf4cbfa8f2535506e4b62e13f3d82e0.png)
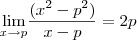 ,
, .
. , basta você multiplicar o limite por
, basta você multiplicar o limite por  no numerador e no denominador que você o resolve.
no numerador e no denominador que você o resolve.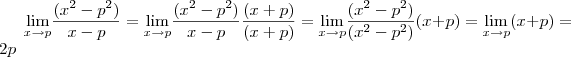
 no limite. Do contrário, como eu mostrei, você terá de utilizar técnicas de resolução de limite desnecessárias nessa etapa do conteúdo.
no limite. Do contrário, como eu mostrei, você terá de utilizar técnicas de resolução de limite desnecessárias nessa etapa do conteúdo. .
. com relação a
com relação a  em um ponto específico , e não em um ponto genérico
em um ponto específico , e não em um ponto genérico  .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.