Estou tentando resolver essa divisão
(6x³-11x²+5x+12 /6x²-7x+12) – (x³+2x-4x-8 / x²- 4)
Consegui chegar até aqui
6x³-11x²+5x+12 /6x²-7x+12
-6x³+7x²-12x x
-4x²+17x
Daí eu não consegui, travei aqui. O que eu estou fazendo errado?
Obrigada, Boa noite



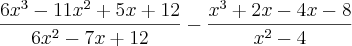


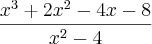
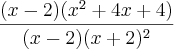
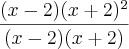




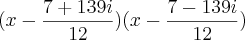 ) e x²- 4=(x+2)(x-2). Agora fatorando as expressões cúbicas: 6x³-11x²+5x+12=(x - 31*(sqrt(3)*%i/2-1/2)/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)*(-sqrt(3)*%i/2-1/2)+11/18) (x - (sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)*(sqrt(3)*%i/2-1/2)+31*(-sqrt(3)*%i/2-1/2)/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+11/18 ) (x- (sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)+31/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+11/18 ) e x³+2x-4x-8=(x-2)*(x+2)^2 .
) e x²- 4=(x+2)(x-2). Agora fatorando as expressões cúbicas: 6x³-11x²+5x+12=(x - 31*(sqrt(3)*%i/2-1/2)/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)*(-sqrt(3)*%i/2-1/2)+11/18) (x - (sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)*(sqrt(3)*%i/2-1/2)+31*(-sqrt(3)*%i/2-1/2)/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+11/18 ) (x- (sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3)+31/(324*(sqrt(147335)/(8*3^(7/2))-2993/2916)^(1/3))+11/18 ) e x³+2x-4x-8=(x-2)*(x+2)^2 .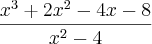
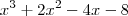



 aparece dos dois lados (antes e depois do sinal de - ; Repare também que tanto o
aparece dos dois lados (antes e depois do sinal de - ; Repare também que tanto o  , quanto o
, quanto o  estão sendo multiplicados pelo
estão sendo multiplicados pelo 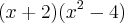
 pode ser escrito como:
pode ser escrito como:  . Logo,
. Logo,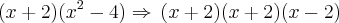
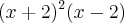

 .
.
 :
: