 por Erickvilela » Sex Fev 22, 2013 21:58
por Erickvilela » Sex Fev 22, 2013 21:58
entao, estou tentando fazer uma questão do livro de guidorizzi de calculo I, entretanto não estou conseguindo
gostaria de pedir ajuda.
a questão é : Prove que a equação x^3 _ 3x^2 + 6 = 0 admite uma unica raíz real. Determine um intervalo de amplitude 1 que contenha tal raiz.
como faço ?
-
Erickvilela
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Fev 14, 2013 21:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sex Fev 22, 2013 23:15
por e8group » Sex Fev 22, 2013 23:15
Boa noite ,já tentou analisar os intervalos de crescimento e de decrescimento de

através de
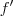
?
Após isto conclua então que pelo TVI existe um

em
![[-2,-1] [-2,-1]](/latexrender/pictures/9b03926afdfad73896be89ba37623f7d.png)
tal que
![f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R} f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R}](/latexrender/pictures/20e5665db757f8cbf7aa9790a0b08356.png)
(OBS.: f é contínua )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Erickvilela » Sex Fev 22, 2013 23:25
por Erickvilela » Sex Fev 22, 2013 23:25
mas tipo, quando eu calculo f ' , vou ter:
3x^2 - 6x = 0, então x=2 e x=0, logo, os intervalos de crescimento e decrescimento vão ser:
cresce em ]-? , 0] e [2, +?[ ; e decresce em [0,2], mas como encontro o intervalo das raízes ?
-
Erickvilela
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Fev 14, 2013 21:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Fev 23, 2013 13:35
por e8group » Sáb Fev 23, 2013 13:35
Considerando
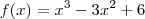
Temos

é estritamente crescente em
![I_1 = ]-\infty ,0] I_1 = ]-\infty ,0]](/latexrender/pictures/d8ce6acc624a27ef7489e70f5d73ef8c.png)
e

e decrescente
![I_ 3 = [0,2] I_ 3 = [0,2]](/latexrender/pictures/6404bf1ec78b8dcfd6431df56759dd09.png)
.
Vamos verificar em cada intervalo

se há pelo menos um

em algum deles tal que

.
(1)
Como

, o termo dominante, possui grau impar ,

e
como

Assim ,existem

tais que

e

.Como

é contínua (Porque ? ) ,pelo TVI existe
![c \in [a,b] \subset I_1 c \in [a,b] \subset I_1](/latexrender/pictures/39388d28b38e710f4837403df0a7620a.png)
tal que
![f(c) = 0 \in [f(a),f(b)] f(c) = 0 \in [f(a),f(b)]](/latexrender/pictures/bf5bc82f80c34ebc04ba55cc717d6e57.png)
.
(2)
Como
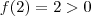
e
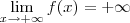
(Porque ?),concluímos que pelo TVI não existe

em
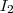
tal que

.
(3)
Segue de imediato de (1) e (2) que

e
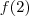
são ambos postivos ,sendo assim,
![0\notin [f(2),f(0)] 0\notin [f(2),f(0)]](/latexrender/pictures/e5d696bb5b221fdcd8d083947e8fa716.png)
, ou seja , não existe

em
![[0,
2] [0,
2]](/latexrender/pictures/5972b6c9e097c358fbe29f611f3dfd56.png)
tal que

.
Conclusão :

admite uma única raiz real ,pois, como já mencionado acima

é estritamente crescente em
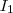
.

Para determinarmos o intervalo de amplitude 1 que contenha

,
veja que
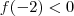
e
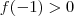
;assim
![\exists c \in [-2,-1] : f(c) = 0 \exists c \in [-2,-1] : f(c) = 0](/latexrender/pictures/1d757c5f4778d0217d58b052ec8df660.png)
.
Espero que ajude .
Editado erro de digitação .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNICAMP) Raíz real positiva
por Carolziiinhaaah » Sex Fev 04, 2011 15:32
- 0 Respostas
- 1213 Exibições
- Última mensagem por Carolziiinhaaah

Sex Fev 04, 2011 15:32
Álgebra Elementar
-
- (POLIEDRO) Única raiz real
por Carolziiinhaaah » Sex Fev 04, 2011 15:33
- 0 Respostas
- 1151 Exibições
- Última mensagem por Carolziiinhaaah

Sex Fev 04, 2011 15:33
Álgebra Elementar
-
- [Derivada]Prove que uma equação tem uma única raiz real .
por e8group » Sex Jun 01, 2012 14:26
- 2 Respostas
- 8401 Exibições
- Última mensagem por e8group

Sex Jun 01, 2012 17:56
Cálculo: Limites, Derivadas e Integrais
-
- [Limites de funções com raíz]
por yakini » Dom Fev 10, 2013 11:32
- 2 Respostas
- 1894 Exibições
- Última mensagem por yakini

Dom Fev 10, 2013 16:17
Cálculo: Limites, Derivadas e Integrais
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3267 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 através de
através de 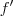 ?
? em
em ![[-2,-1] [-2,-1]](/latexrender/pictures/9b03926afdfad73896be89ba37623f7d.png) tal que
tal que ![f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R} f(c) = 0 \in [f(2),f(-1)]\subset D_f =\mathbb{R}](/latexrender/pictures/20e5665db757f8cbf7aa9790a0b08356.png) (OBS.: f é contínua )
(OBS.: f é contínua )
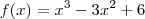
![I_1 = ]-\infty ,0] I_1 = ]-\infty ,0]](/latexrender/pictures/d8ce6acc624a27ef7489e70f5d73ef8c.png) e
e  e decrescente
e decrescente ![I_ 3 = [0,2] I_ 3 = [0,2]](/latexrender/pictures/6404bf1ec78b8dcfd6431df56759dd09.png) .
. se há pelo menos um
se há pelo menos um  .
. , o termo dominante, possui grau impar ,
, o termo dominante, possui grau impar , 

 tais que
tais que  e
e  .Como
.Como ![c \in [a,b] \subset I_1 c \in [a,b] \subset I_1](/latexrender/pictures/39388d28b38e710f4837403df0a7620a.png) tal que
tal que ![f(c) = 0 \in [f(a),f(b)] f(c) = 0 \in [f(a),f(b)]](/latexrender/pictures/bf5bc82f80c34ebc04ba55cc717d6e57.png) .
. 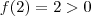 e
e 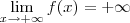 (Porque ?),concluímos que pelo TVI não existe
(Porque ?),concluímos que pelo TVI não existe 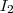 tal que
tal que  e
e 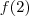 são ambos postivos ,sendo assim,
são ambos postivos ,sendo assim, ![0\notin [f(2),f(0)] 0\notin [f(2),f(0)]](/latexrender/pictures/e5d696bb5b221fdcd8d083947e8fa716.png) , ou seja , não existe
, ou seja , não existe ![[0,
2] [0,
2]](/latexrender/pictures/5972b6c9e097c358fbe29f611f3dfd56.png) tal que
tal que 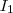 .
.
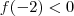 e
e 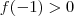 ;assim
;assim ![\exists c \in [-2,-1] : f(c) = 0 \exists c \in [-2,-1] : f(c) = 0](/latexrender/pictures/1d757c5f4778d0217d58b052ec8df660.png) .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.