Estou com o seguinte problema:
Calcular a integral
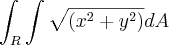 sendo R a região interna a circunferência de centro (0,1) e raio 1, e entre as retas y=x e x=0 (usar coordenadas polares).
sendo R a região interna a circunferência de centro (0,1) e raio 1, e entre as retas y=x e x=0 (usar coordenadas polares).A área é essa:
Minha primeira tentativa foi dividir em duas regiões R1 e R2, sendo:
R1: O quarto de circulo superior, ficando:

e
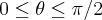
R2: O quarto de cirulo inferior, ficando:
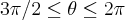
Porém eu esbarro na hora de definir os limites do "r", pois a reta x=y eu não consigo transformar para polar.
Alguma dica para me ajudar?


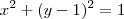







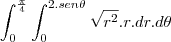
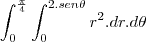

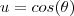

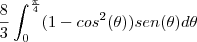
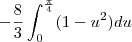
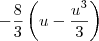

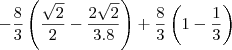

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.