 por paulorobertoqf » Qua Fev 20, 2013 14:05
por paulorobertoqf » Qua Fev 20, 2013 14:05
Se, para dados n, m
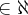
, o limite

é finito e não nulo, então seu valor deve ser igual a:
Resposta: 3
Pessoal, estou estudando limites mas não consegui chegar a este resultado. Tentei fazer pelo teorema de L'hopital, mas nunca dá certo. Até o professor não sabe como faz. Poderiam ajudar??
-
paulorobertoqf
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 20, 2013 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Qua Fev 20, 2013 20:39
por young_jedi » Qua Fev 20, 2013 20:39
pelo teorema de l'Hospital


neste caso temos tres possibilidades caso m seja maior que n então este limite tende para zero
se n é maior que m então o limite tende para infinito
mais se m é igual a n então o limite é igual a tres
como o enunciado diz que o limite é finito e não nulol, então so podemos ter o terceiro caso onde n=m e portanto o limite é igual a 3
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por paulorobertoqf » Qua Fev 20, 2013 20:49
por paulorobertoqf » Qua Fev 20, 2013 20:49
Muito bom.... obrigado pela pronta explicação!!
Vou continuar meus estudos.
Valeu!
-
paulorobertoqf
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 20, 2013 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6646 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5122 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7264 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4440 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
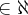 , o limite
, o limite  é finito e não nulo, então seu valor deve ser igual a:
é finito e não nulo, então seu valor deve ser igual a:




