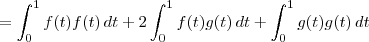por Claudin » Qua Fev 20, 2013 02:01
por Claudin » Qua Fev 20, 2013 02:01
Calcule

Definição do produto interno:
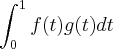
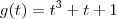
e
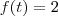
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Fev 20, 2013 09:33
por LuizAquino » Qua Fev 20, 2013 09:33
Claudin escreveu:Calcule

Definição do produto interno:
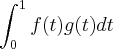
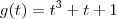
e
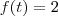
Como você já deve saber, temos que uma das propriedades do produto interno é:
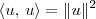
Usando então essa propriedade, temos que:

Usando a definição de produto interno que foi dada, temos que:
![\int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \|f(t) + g(t)\|^2 \int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \|f(t) + g(t)\|^2](/latexrender/pictures/39a59e416a0b6303f055363c0dd1d3e6.png)
Substituindo as expressões de f(t) e g(t) que foram dadas, podemos obter:

Agora tente concluir o exercício a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Fev 20, 2013 10:08
por Claudin » Qua Fev 20, 2013 10:08
O correto nao seria
![||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}= ||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}=](/latexrender/pictures/77858ec582a72d409e196d2cde59a3d1.png)
![\sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)} \sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)}](/latexrender/pictures/d5720528c712b8527451cb1acdcc45a4.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Fev 20, 2013 10:27
por LuizAquino » Qua Fev 20, 2013 10:27
Claudin escreveu:O correto nao seria
![||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}= ||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}=](/latexrender/pictures/77858ec582a72d409e196d2cde59a3d1.png)
![\sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)} \sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)}](/latexrender/pictures/d5720528c712b8527451cb1acdcc45a4.png)
Apenas corrigindo o que você escreveu, temos que:
Agora pense um pouco... Se você sabe que
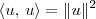
, então fica claro que
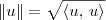
. Desse modo, você pode usar qualquer uma das duas formas.
E pesando mais um pouco, você pode perceber que:
![\int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \int_0^1 f(t)f(t) +2f(t)g(t) + g(t)g(t)\, dt \int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \int_0^1 f(t)f(t) +2f(t)g(t) + g(t)g(t)\, dt](/latexrender/pictures/c793723bd40e6b72af09ca78c26e0f41.png)
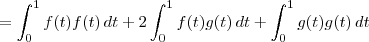

Conclusão: o que eu fiz é equivalente ao que você tentou dizer.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto Interno
por Claudin » Sáb Fev 16, 2013 15:50
- 2 Respostas
- 2468 Exibições
- Última mensagem por Claudin

Ter Fev 19, 2013 21:05
Álgebra Linear
-
- Produto Interno
por iarapassos » Seg Mar 18, 2013 13:42
- 0 Respostas
- 1484 Exibições
- Última mensagem por iarapassos

Seg Mar 18, 2013 13:42
Álgebra Linear
-
- Produto Interno Euclidiano
por ARCS » Sáb Dez 10, 2011 17:57
- 1 Respostas
- 2096 Exibições
- Última mensagem por MarceloFantini

Dom Dez 11, 2011 04:06
Geometria Analítica
-
- Produto Interno Usual
por iarapassos » Qui Mar 21, 2013 00:04
- 1 Respostas
- 1725 Exibições
- Última mensagem por Ge_dutra

Qui Mar 21, 2013 00:46
Álgebra Linear
-
- Produto Interno - Vetores Ortogonais
por iarapassos » Qui Mar 21, 2013 00:02
- 1 Respostas
- 1758 Exibições
- Última mensagem por Russman

Qui Mar 21, 2013 12:14
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

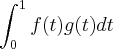
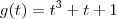 e
e 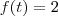


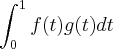
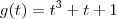 e
e 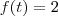

e
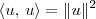

![\int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \|f(t) + g(t)\|^2 \int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \|f(t) + g(t)\|^2](/latexrender/pictures/39a59e416a0b6303f055363c0dd1d3e6.png)


![||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}= ||f(t)+g(t)||=\sqrt[]{<f(t)+g(t)>}=](/latexrender/pictures/77858ec582a72d409e196d2cde59a3d1.png)
![\sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)} \sqrt[]{(<f(t),f(t)>+2<f(t)+g(t)+<g(t)+g(t)>)}](/latexrender/pictures/d5720528c712b8527451cb1acdcc45a4.png)

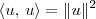 , então fica claro que
, então fica claro que 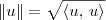 . Desse modo, você pode usar qualquer uma das duas formas.
. Desse modo, você pode usar qualquer uma das duas formas.![\int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \int_0^1 f(t)f(t) +2f(t)g(t) + g(t)g(t)\, dt \int_0^1 [f(t)+g(t)][f(t)+g(t)]\, dt = \int_0^1 f(t)f(t) +2f(t)g(t) + g(t)g(t)\, dt](/latexrender/pictures/c793723bd40e6b72af09ca78c26e0f41.png)