 por Georges123 » Sáb Fev 16, 2013 00:20
por Georges123 » Sáb Fev 16, 2013 00:20
Três grandes amigos, cada um deles com algum dinheiro, redistribuem o que possuem da seguinte maneira: Antonio dá a Bernado e a Carlos dinheiro suficiente para duplicar a quantia que cada um possui. A seguir, Bernado dá a Antonio e a Carlos o suficiente para que cada um duplique a quantia que possui. Finalmente, Carlos faz o mesmo, isto é, dá a Antonio E A Bernado o suficiente para que cada um duplique a quantia que possui. Se Carlos possuía 36,00(REAIS) tanto no início quanto no final da distribuição,qual a quantia total que os três amigos possuem juntos?
Eu pensei da seguinte forma: e não consegui desenvolver mais
Antonio:A, Bernado:B Carlos:C = 36
A+X=2A
B+X=2B
C+X=2C
A-X=B+X
A-X=C+X
B-X=A+X
B-X=C+X
C-X=A+X
C-X=B+X
dessa forma saiu que o x é igual a 36 e não pode ser poix c-x=b+x b seria o, Acho que não foram as mesmas quantias retiradas em dinheiro
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sáb Fev 16, 2013 11:31
por young_jedi » Sáb Fev 16, 2013 11:31
no inicio as quantias são A, B, C
apos a primeira distriguição passa a ser
A-B-C
2B
2C
apos a segunda redistribuinção
2A-2B-2C
2B-(A-B-C)-2C=3B-A-C
4C
e apos a terceira
4A-4B-4C
6B-2A-2C
4C-(2A-2B-2C)-(3B-A-C)=7C-A-B
como calrlos possuia 36 tanto no inicio quanto no final então


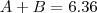
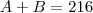
portanto
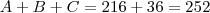
portanto eles possuem juntos 252,00 reais
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Georges123 » Dom Fev 17, 2013 17:09
por Georges123 » Dom Fev 17, 2013 17:09
Obrigado, que deus te abençoe
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema simples de operações com números naturais - EF
por juliahess » Ter Jul 31, 2012 12:55
- 1 Respostas
- 1279 Exibições
- Última mensagem por DanielFerreira

Ter Jul 31, 2012 21:26
Álgebra Elementar
-
- ajuda neste problema envolvendo numeros racionais.
por angelmix » Qua Out 19, 2011 17:02
- 0 Respostas
- 1902 Exibições
- Última mensagem por angelmix

Qua Out 19, 2011 17:02
Álgebra Elementar
-
- números naturais
por jose henrique » Dom Ago 15, 2010 15:24
- 2 Respostas
- 1704 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 10:40
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 11:44
- 0 Respostas
- 1176 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 11:44
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 12:31
- 1 Respostas
- 1627 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




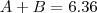
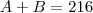
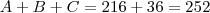



 , avisa que eu resolvo.
, avisa que eu resolvo.

