por Rafael Pitzer » Seg Fev 11, 2013 18:54
1- ? = 180-y + 180-?
2- ? = 180-y + 180-?
3- ? = y + 180-?
4- ? = y + 180-?
y = 180-?+180-?
substituindo o y em 3 por exemplo
? = 180-?+180-?+180-? efetuando a soma de ? nos dois lados
?+? = 180-?+180+180-? efetuando a soma de ? nos dois lados
?+?+? = 180+180+180-? efetuando a soma de ? nos dois lados
?+?+?+? = 180+180+180
?+?+?+? = 540°
Gostaria de saber se o meu raciocínio está correto.
-
Rafael Pitzer
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Qua Jan 30, 2013 12:12
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
por young_jedi » Seg Fev 11, 2013 20:36
amigo eu calculei aqui usando um procedimento diferente e o resultado deu esse mesmo
540º , porem não entendi como voce chegou nas relações das primeiras equações que voce colocou, se tivesse com demonstrar, ficaria grato.
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
por DanielFerreira » Ter Fev 12, 2013 12:54
Rafael,
seu raciocínio está correto!
Young_jedi,
o Rafael fez o seguinte: atribuiu a um dos ângulos uma variável bem parecida com um dos ângulos dado. Confesso que demorei a perceber isso. [risos]!
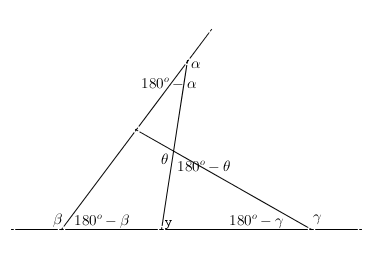
- di.png (9.71 KiB) Exibido 1888 vezes
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
por young_jedi » Ter Fev 12, 2013 13:51
a agora sim entendi, tem uma variavel y, eu estava achando que era
então esta tudo certo
valeu pela demonstração ai
danjr5
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
por DanielFerreira » Ter Fev 12, 2013 17:02
Até a próxima!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão geometria plana relacionada aos ângulos notáveis]
por Anniemf » Qua Mar 28, 2012 14:33
- 1 Respostas
- 3435 Exibições
- Última mensagem por kelvinJhonson
Sáb Abr 21, 2012 23:20
Geometria Plana
-
- Soma dos Ângulos internos.
por sauloandrade » Sáb Dez 29, 2012 21:07
- 5 Respostas
- 4503 Exibições
- Última mensagem por e8group
Dom Dez 30, 2012 17:51
Geometria Plana
-
- Geo. Plana (Ângulos Na Circun.)
por nandokmx » Dom Jul 18, 2010 22:37
- 1 Respostas
- 1238 Exibições
- Última mensagem por MarceloFantini
Seg Jul 19, 2010 03:06
Geometria Plana
-
- [Geometria] Ângulos.
por Lucas Ponte » Qui Nov 03, 2011 15:56
- 1 Respostas
- 1047 Exibições
- Última mensagem por LuizAquino
Dom Nov 06, 2011 18:57
Geometria Analítica
-
- [Geometria] O menor valor possível para soma.
por my2009 » Ter Fev 09, 2016 10:59
- 1 Respostas
- 4454 Exibições
- Última mensagem por Baltuilhe
Sáb Fev 20, 2016 19:27
Geometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
