 por anneliesero » Qua Jan 23, 2013 15:08
por anneliesero » Qua Jan 23, 2013 15:08
Olá, pessoal
poderiam me ajudar nessa questão?
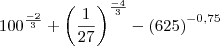
Por onde começo?
Fiz assim não sei se está certo:
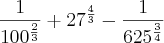
Depois
![\sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}} \sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}}](/latexrender/pictures/9e7499bcb6a0054d6f9251dfcdebda77.png)
Agora nessa parte não consegui fazer:
![\sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3} \sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3}](/latexrender/pictures/095d2783fa8fe857e0e0f1800971713d.png)
Continua fatorando?

''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qua Jan 23, 2013 21:00
por DanielFerreira » Qua Jan 23, 2013 21:00
Oi
Anne,
boa noite!
![\\ 10^{- \frac{2}{3}} + \left( \frac{1}{27}\right)^{- \frac{4}{3}} - 625^{- 0,75} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( \frac{27}{1}\right)^{\frac{4}{3}} - 625^{- \frac{3}{4}} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( 3^3 \right)^{\frac{4}{3}} - \left( \frac{1}{5^4} \right)^{\frac{3}{4}} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[3]{(3^3)^4} - \sqrt[4]{\left( \frac{1}{5^4} \right)^3} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[\cancel{3}]{(3^\cancel{3})^4} - \sqrt[\cancel{4}]{\left( \frac{1}{5^\cancel{4}} \right)^3} = \\\\\\ \frac{1}{\sqrt[3]{100}} + 3^4 - \frac{1}{5^3} = \\ 10^{- \frac{2}{3}} + \left( \frac{1}{27}\right)^{- \frac{4}{3}} - 625^{- 0,75} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( \frac{27}{1}\right)^{\frac{4}{3}} - 625^{- \frac{3}{4}} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( 3^3 \right)^{\frac{4}{3}} - \left( \frac{1}{5^4} \right)^{\frac{3}{4}} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[3]{(3^3)^4} - \sqrt[4]{\left( \frac{1}{5^4} \right)^3} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[\cancel{3}]{(3^\cancel{3})^4} - \sqrt[\cancel{4}]{\left( \frac{1}{5^\cancel{4}} \right)^3} = \\\\\\ \frac{1}{\sqrt[3]{100}} + 3^4 - \frac{1}{5^3} =](/latexrender/pictures/a6ab30211094396485fc6f3b185744c0.png)
Qualquer dúvida, comente!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Rafael16 » Qua Jan 23, 2013 21:27
por Rafael16 » Qua Jan 23, 2013 21:27
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por anneliesero » Qua Jan 23, 2013 22:44
por anneliesero » Qua Jan 23, 2013 22:44
Rafael16 você errou na terceira linha veja a sua resposta:
![\sqrt[3]{{100}^{-2}} = \sqrt[3]{{10}^{-3}} \sqrt[3]{{100}^{-2}} = \sqrt[3]{{10}^{-3}}](/latexrender/pictures/72cc0e6d53a96dea8f7f1c16f9e9f0d4.png)
O correto é:
![\sqrt[3]{{100}^{-2}} = \sqrt[3]{{{(10}^{2)}}^{-2}} \sqrt[3]{{100}^{-2}} = \sqrt[3]{{{(10}^{2)}}^{-2}}](/latexrender/pictures/46312ceeba802171d495e2b062151cfc.png)
Espero que tenha entendido!!
Aliás, obrigado danjr5!!! Consegui entender!!!




''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjuntos numéricos
por Marcampucio » Ter Set 01, 2009 21:50
- 1 Respostas
- 1441 Exibições
- Última mensagem por Elcioschin

Ter Set 01, 2009 22:38
Álgebra Elementar
-
- Conjuntos numericos
por cristina » Seg Set 14, 2009 18:41
- 1 Respostas
- 1625 Exibições
- Última mensagem por Molina

Ter Set 15, 2009 16:07
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:38
- 0 Respostas
- 1214 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:38
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:40
- 0 Respostas
- 1250 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:40
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:42
- 0 Respostas
- 1051 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
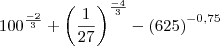
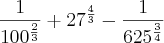
![\sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}} \sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}}](/latexrender/pictures/9e7499bcb6a0054d6f9251dfcdebda77.png)
![\sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3} \sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3}](/latexrender/pictures/095d2783fa8fe857e0e0f1800971713d.png)


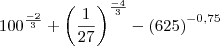
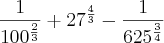
![\sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}} \sqrt[3]{{100}^{2}} + \sqrt[3]{{27}^{4}} - \sqrt[4]{{625}^{3}}](/latexrender/pictures/9e7499bcb6a0054d6f9251dfcdebda77.png)
![\sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3} \sqrt[3]{{1000}} + \sqrt[3]{{531441}} - \sqrt[4]{\left({25}^{2} \right)}{}^{3}](/latexrender/pictures/095d2783fa8fe857e0e0f1800971713d.png)


![\\ 10^{- \frac{2}{3}} + \left( \frac{1}{27}\right)^{- \frac{4}{3}} - 625^{- 0,75} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( \frac{27}{1}\right)^{\frac{4}{3}} - 625^{- \frac{3}{4}} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( 3^3 \right)^{\frac{4}{3}} - \left( \frac{1}{5^4} \right)^{\frac{3}{4}} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[3]{(3^3)^4} - \sqrt[4]{\left( \frac{1}{5^4} \right)^3} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[\cancel{3}]{(3^\cancel{3})^4} - \sqrt[\cancel{4}]{\left( \frac{1}{5^\cancel{4}} \right)^3} = \\\\\\ \frac{1}{\sqrt[3]{100}} + 3^4 - \frac{1}{5^3} = \\ 10^{- \frac{2}{3}} + \left( \frac{1}{27}\right)^{- \frac{4}{3}} - 625^{- 0,75} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( \frac{27}{1}\right)^{\frac{4}{3}} - 625^{- \frac{3}{4}} = \\\\\\ \left( \frac{1}{10}\right)^{\frac{2}{3}} + \left( 3^3 \right)^{\frac{4}{3}} - \left( \frac{1}{5^4} \right)^{\frac{3}{4}} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[3]{(3^3)^4} - \sqrt[4]{\left( \frac{1}{5^4} \right)^3} = \\\\\\ \sqrt[3]{\left( \frac{1}{10} \right)^2} + \sqrt[\cancel{3}]{(3^\cancel{3})^4} - \sqrt[\cancel{4}]{\left( \frac{1}{5^\cancel{4}} \right)^3} = \\\\\\ \frac{1}{\sqrt[3]{100}} + 3^4 - \frac{1}{5^3} =](/latexrender/pictures/a6ab30211094396485fc6f3b185744c0.png)

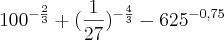
![\sqrt[3]{100^{-2}} + \sqrt[3]{27^{-4}} - {625}^{-\frac{75}{100}}} \sqrt[3]{100^{-2}} + \sqrt[3]{27^{-4}} - {625}^{-\frac{75}{100}}}](/latexrender/pictures/a130b0b1a6969594fbb53e67f8d4ab2c.png)
![\sqrt[3]{{10}^{-3}} + \sqrt[3]{({3}^{3})^{-4}} - \sqrt[100]{{625}^{-75}} \sqrt[3]{{10}^{-3}} + \sqrt[3]{({3}^{3})^{-4}} - \sqrt[100]{{625}^{-75}}](/latexrender/pictures/f8e31df13257aa7dfb83180568e0967f.png)
![{10}^{-1} + \sqrt[3]{{3}^{-12}} - \sqrt[\frac{100}{25}]{{625}^{-\frac{75}{25}}} {10}^{-1} + \sqrt[3]{{3}^{-12}} - \sqrt[\frac{100}{25}]{{625}^{-\frac{75}{25}}}](/latexrender/pictures/3e9bf82d67304b4a8e4790d34b20a908.png)
![\frac{1}{10} + {3}^{-4} - \sqrt[4]{625^{-3}} \frac{1}{10} + {3}^{-4} - \sqrt[4]{625^{-3}}](/latexrender/pictures/90d8e88213bda9abfa1a91081ca383c7.png)
![\frac{1}{10} + \frac{1}{81} - \sqrt[4]{(5^{4})^{-3}} \frac{1}{10} + \frac{1}{81} - \sqrt[4]{(5^{4})^{-3}}](/latexrender/pictures/8fd7894fdd64f9a302abfb329ffefd44.png)
![\frac{1}{10} + \frac{1}{81} - \sqrt[4]{5^{-12}} \frac{1}{10} + \frac{1}{81} - \sqrt[4]{5^{-12}}](/latexrender/pictures/bfc6bb4104917b9adf1b6b9b04c86943.png)
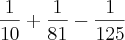
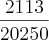

![\sqrt[3]{{100}^{-2}} = \sqrt[3]{{10}^{-3}} \sqrt[3]{{100}^{-2}} = \sqrt[3]{{10}^{-3}}](/latexrender/pictures/72cc0e6d53a96dea8f7f1c16f9e9f0d4.png)
![\sqrt[3]{{100}^{-2}} = \sqrt[3]{{{(10}^{2)}}^{-2}} \sqrt[3]{{100}^{-2}} = \sqrt[3]{{{(10}^{2)}}^{-2}}](/latexrender/pictures/46312ceeba802171d495e2b062151cfc.png)




