 por Claudin » Sáb Jan 19, 2013 09:38
por Claudin » Sáb Jan 19, 2013 09:38
To com dúvida em algumas integrais.
São todas simples, que eu já até fiz, porém fui refazer, e não to encontrando o resultado correto.
1 -
![\int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx \int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx](/latexrender/pictures/f8d8717c1d6e4a07e3b9e8e6005d43a0.png)
2 -
![\int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy \int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy](/latexrender/pictures/3e514e2691732eedbf8a210c75a32338.png)
3 -
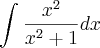
Encontrei na
1 -
![2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c 2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c](/latexrender/pictures/d652763acb1e89823c07a88b46052f54.png)
2 -
![\frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c \frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c](/latexrender/pictures/41ffdac2384fd875506c1de798d71abf.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Jan 21, 2013 22:17
por Cleyson007 » Seg Jan 21, 2013 22:17
Boa noite Claudin!
Resolução da primeira questão:

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5635 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2714 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3992 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5056 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2069 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx \int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx](/latexrender/pictures/f8d8717c1d6e4a07e3b9e8e6005d43a0.png)
![\int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy \int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy](/latexrender/pictures/3e514e2691732eedbf8a210c75a32338.png)
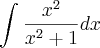
![2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c 2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c](/latexrender/pictures/d652763acb1e89823c07a88b46052f54.png)
![\frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c \frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c](/latexrender/pictures/41ffdac2384fd875506c1de798d71abf.png)

![\int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx \int_{}^{}(\frac{1}{\sqrt[]{x}}+\frac{x\sqrt[]{x}}{3})dx](/latexrender/pictures/f8d8717c1d6e4a07e3b9e8e6005d43a0.png)
![\int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy \int_{}^{}(\sqrt[]{2y}-\frac{1}{\sqrt[]{2y}})dy](/latexrender/pictures/3e514e2691732eedbf8a210c75a32338.png)
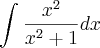
![2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c 2\sqrt[]{x}+\frac{2}{9}\sqrt[]{x}+c](/latexrender/pictures/d652763acb1e89823c07a88b46052f54.png)
![\frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c \frac{2}{3}\sqrt[]{2y^3}-\sqrt[]{2y}+c](/latexrender/pictures/41ffdac2384fd875506c1de798d71abf.png)



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
