1)Esboce a regi ?o e ache a areá da região compreendida entre:
a)os gráficos de f (x) =

b)os graficos de f(x) =

c)os graficos de f(x) =
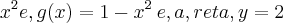
2) esboce o conjunto D e ache a area de D,nos seguintes casos
a) D = ( x,y)


b) D = ( x,y)
 R^2 ;
R^2 ; 



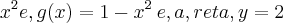


 R^2 ;
R^2 ; 

 , em verde, e
, em verde, e 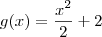 , em vermelho.
, em vermelho. , de modo que
, de modo que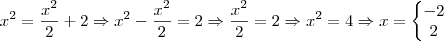
 e
e 
 e a função
e a função  e subtrairmos da área entre o eixo
e subtrairmos da área entre o eixo  e a função
e a função  no intervalo
no intervalo ![[-2,2] [-2,2]](/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png) teremos isolado a região de interesse.
teremos isolado a região de interesse.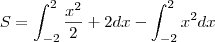
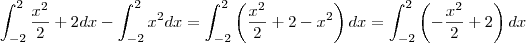

 estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o
estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o 






Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)