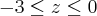por manuel_pato1 » Sex Jan 18, 2013 00:34
por manuel_pato1 » Sex Jan 18, 2013 00:34
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados:
a)
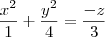
no intervado
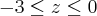
Alguém pode me dar uma luz? como devoo proceder para conseguir uma superfície somente no intervalo dado?
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Sex Jan 18, 2013 00:49
por Russman » Sex Jan 18, 2013 00:49
Isto é uma fatia de um parabolóide elíptico.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuel_pato1 » Sex Jan 18, 2013 22:54
por manuel_pato1 » Sex Jan 18, 2013 22:54
Ok, mas como eu procedo para resolver esse tipo de exerício, mostrando algebricamente que é um parabolóide elíptico?
tenho que chutar z= 0 , z= -3 e um valor intermediário entre o intervalo?
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Sex Jan 18, 2013 23:00
por Russman » Sex Jan 18, 2013 23:00
Não sei se a intenção é "mostrar algebricamente" que é um paraboloide elíptico. A curva dada por essa equação DEFINE-SE como um paraboloide elíptico. É um nome que se dá a esse tipo de curva com essa equação. Logo, basta reconhece-la.
O que você pode argumentar é que os denominadores de x² e y² são diferentes, logo é algo elíptico. E ainda como z aparece sem potência, nessa combinação, é um paraboloide.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuel_pato1 » Sex Jan 18, 2013 23:08
por manuel_pato1 » Sex Jan 18, 2013 23:08
Entendi cara. Brigadão hein!
Acho que onde eu tenho que chutar alguns valor é pra hora que eu for desenhar no R³
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Sex Jan 18, 2013 23:13
por Russman » Sex Jan 18, 2013 23:13
É, pra desenhar essa curva seria interessante, como pede, você delimita-la entre z=-3 e z=0. Substituindo esses valores na equação você vai ter a curva plana de x e y. Uma é uma elipse e outra um ponto.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quadricas Centradas
por ah001334 » Ter Nov 15, 2011 13:21
- 3 Respostas
- 2208 Exibições
- Última mensagem por ah001334

Ter Nov 15, 2011 23:19
Geometria Analítica
-
- Cônicas e quádricas
 por Danilo » Ter Jan 08, 2013 13:25
por Danilo » Ter Jan 08, 2013 13:25
- 2 Respostas
- 5118 Exibições
- Última mensagem por Danilo

Qui Abr 04, 2013 00:43
Geometria Analítica
-
- Cônicas e quádricas
por Danilo » Ter Jan 08, 2013 13:27
- 1 Respostas
- 1398 Exibições
- Última mensagem por manuel_pato1

Qui Jan 17, 2013 23:18
Geometria Analítica
-
- Questões de cônicas e quádricas
por sorchilas » Sáb Dez 11, 2010 12:55
- 9 Respostas
- 7485 Exibições
- Última mensagem por sorchilas

Seg Dez 13, 2010 12:30
Geometria Analítica
-
- (Quadricas) equação da superfície
por manuel_pato1 » Ter Dez 04, 2012 18:47
- 1 Respostas
- 4390 Exibições
- Última mensagem por young_jedi

Ter Dez 04, 2012 21:33
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
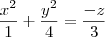 no intervado
no intervado 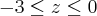

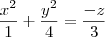 no intervado
no intervado