 por RODRIGO DE FARIA » Qui Jan 17, 2013 00:34
por RODRIGO DE FARIA » Qui Jan 17, 2013 00:34
COMO CALCULAR A MULTIPLICAÇAO DE EXPOENTES
5^25 X 7^35
-
RODRIGO DE FARIA
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 17, 2013 00:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabilidade
- Andamento: formado
 por Russman » Qui Jan 17, 2013 00:46
por Russman » Qui Jan 17, 2013 00:46
Se a base for igual então basta somar os expoentes.

Mas como não é o caso, temos

e

, você só pode simplificar essa expressão usando o fato de que

.
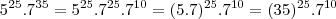
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por ant_dii » Qui Jan 17, 2013 01:09
por ant_dii » Qui Jan 17, 2013 01:09
Tem como você fazer assim:

Só não sei se ajudará muito pois será um número enorme...
Qualquer coisa simplifica só...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por RODRIGO DE FARIA » Sex Jan 25, 2013 12:29
por RODRIGO DE FARIA » Sex Jan 25, 2013 12:29
Obrigado -
Não ha como chegar ao resultado final?
Sem precisar fazer esta multiplicaçao com expoentes elevados?
-
RODRIGO DE FARIA
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 17, 2013 00:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: contabilidade
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equaçao com expoentes
por tajas » Dom Mai 06, 2012 11:21
- 1 Respostas
- 2022 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 15:54
Sistemas de Equações
-
- Log e expoentes fracionários
por sergioereis1 » Dom Abr 20, 2014 06:51
- 0 Respostas
- 2344 Exibições
- Última mensagem por sergioereis1

Dom Abr 20, 2014 06:51
Logaritmos
-
- Simplicação trabalhando expoentes.
por Rafael Sposito » Dom Fev 17, 2013 17:51
- 1 Respostas
- 1446 Exibições
- Última mensagem por young_jedi

Dom Fev 17, 2013 23:47
Álgebra Elementar
-
- Potencias com expoentes diferentes - Subtrair?
por Soprano » Dom Fev 14, 2016 10:25
- 7 Respostas
- 7586 Exibições
- Última mensagem por Soprano

Dom Fev 14, 2016 17:05
Números Complexos
-
- [DÚVIDA] Potências de expoentes racionais e raízes.
por invader_zim » Ter Fev 12, 2013 11:31
- 3 Respostas
- 2343 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 12:24
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 e
e  , você só pode simplificar essa expressão usando o fato de que
, você só pode simplificar essa expressão usando o fato de que  .
.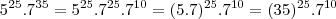





 .
.



