 por thejotta » Sex Jan 11, 2013 10:10
por thejotta » Sex Jan 11, 2013 10:10
- Código: Selecionar todos
ty'+2y-cos(t)/t =0 y(t0)=y0
Ache uma solução dessa PVI(Problema de valor inicial)
tentei fazer da seguinte maneira reajustei a formula que ficou assim
- Código: Selecionar todos
y'=(cos(t) - 2yt)/t^2
depois tentei integrar cada lado da função mais não conseguir resolver e tambem não sei se estou indo pelo caminho certo.
alguem poderia me ajudar.
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Sex Jan 11, 2013 12:12
por young_jedi » Sex Jan 11, 2013 12:12
Nesta EDO voce tem que utilizar o metodo do fator integrante.
Não sei se voce ja estudou ete metodo de resolução, comente qualquer coisa.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thejotta » Sex Jan 11, 2013 13:07
por thejotta » Sex Jan 11, 2013 13:07
Não ainda não estudei
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Sex Jan 11, 2013 15:09
por young_jedi » Sex Jan 11, 2013 15:09
Editado pela última vez por
young_jedi em Sex Jan 11, 2013 18:15, em um total de 1 vez.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thejotta » Sex Jan 11, 2013 17:58
por thejotta » Sex Jan 11, 2013 17:58
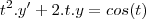
mais temos que

//Não entendi o pq disso?
então

-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Sex Jan 11, 2013 18:14
por young_jedi » Sex Jan 11, 2013 18:14
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thejotta » Sex Jan 11, 2013 23:41
por thejotta » Sex Jan 11, 2013 23:41
Muito obrigado mesmo... acabei tmb lendo sobre o metodo do fator integrante e conseguir resolver, mais ainda ficou uma duvida sobre a substituição do valor inicial.. como faz para achar Y(t0)=v0 e os valores de t0 r v0?
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Sáb Jan 12, 2013 09:53
por young_jedi » Sáb Jan 12, 2013 09:53
substitua y0 e t0 na equação e encontre a constante c em função desses dois valores ai voce tera a equação completa
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por thejotta » Dom Jan 13, 2013 11:22
por thejotta » Dom Jan 13, 2013 11:22
Muito obrigado amigo
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teorema do Residuo de Cauchy]
por Gebe » Qua Jun 03, 2015 23:27
- 2 Respostas
- 3394 Exibições
- Última mensagem por adauto martins

Qua Mar 02, 2016 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Limite de sequências - Teste de Cauchy
por valeuleo » Seg Nov 21, 2011 16:27
- 1 Respostas
- 1828 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 10:17
Cálculo: Limites, Derivadas e Integrais
-
- Análise Real : Números Reais (desigualdade de Cauchy-Schwar
por JorgeVidal » Dom Fev 22, 2015 18:00
- 1 Respostas
- 3637 Exibições
- Última mensagem por adauto martins

Qua Fev 25, 2015 20:49
Teoria dos Números
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10718 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9730 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





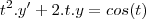




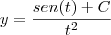
 //Não entendi o pq disso?
//Não entendi o pq disso? 
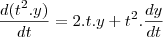
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
