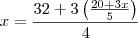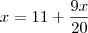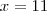por sadzinski » Qua Jan 02, 2013 18:55
por sadzinski » Qua Jan 02, 2013 18:55
Quando uma empresa usa x unidades de trabalho e y unidades de capital, sua produção mensal de certo produto é dado por f(x,y)= 32x +20y +3xy -2x² -2,5y². Obtenha os valeres de x e y que maximizam o lucro.
Minha duvida é: a função f(x,y), já esta pronta para ser derivar parcialmente?
As raízes vão me dizer quais são os maxímos e os minimos?
-
sadzinski
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 01, 2013 16:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Fabricação Mecânica
- Andamento: cursando
 por Russman » Qua Jan 02, 2013 21:56
por Russman » Qua Jan 02, 2013 21:56
Você precisa obter a função Lucro (

) e então basta que você resolva o sistema

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por young_jedi » Qua Jan 09, 2013 20:36
por young_jedi » Qua Jan 09, 2013 20:36
veja que voce chegou na seguinte relação
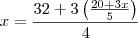
resolvendo voce chega em
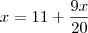
ai nesta parte voce se confundiu, o correto seria


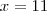
corrija o resto
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Qua Jan 09, 2013 21:11
por Russman » Qua Jan 09, 2013 21:11
Acredito que houve um erro de digitação, pois x= 20.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por sadzinski » Qui Jan 10, 2013 05:34
por sadzinski » Qui Jan 10, 2013 05:34
Obrigado pela ajuda.
-
sadzinski
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 01, 2013 16:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Fabricação Mecânica
- Andamento: cursando
 por young_jedi » Qui Jan 10, 2013 10:39
por young_jedi » Qui Jan 10, 2013 10:39
verdade
x=20
me confundi na ultima expressão
obrigado por observar russman
valeu ate mais
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Otimização calculo 2
por sadzinski » Qua Jan 09, 2013 17:52
- 0 Respostas
- 744 Exibições
- Última mensagem por sadzinski

Qua Jan 09, 2013 17:52
Cálculo: Limites, Derivadas e Integrais
-
- Otimização calculo 2 ( Um edifício )
por sadzinski » Ter Jan 15, 2013 08:47
- 1 Respostas
- 2997 Exibições
- Última mensagem por young_jedi

Ter Jan 15, 2013 15:04
Cálculo: Limites, Derivadas e Integrais
-
- Otimização calculo 2 (retângulo inscrito em um triângulo)
 por sadzinski » Qui Jan 03, 2013 08:39
por sadzinski » Qui Jan 03, 2013 08:39
- 1 Respostas
- 9449 Exibições
- Última mensagem por young_jedi

Qui Jan 03, 2013 11:34
Cálculo: Limites, Derivadas e Integrais
-
- Otimização calculo 2 ( O lucro que uma empresa obtém)
 por sadzinski » Qui Jan 10, 2013 11:42
por sadzinski » Qui Jan 10, 2013 11:42
- 3 Respostas
- 4071 Exibições
- Última mensagem por young_jedi

Sex Jan 11, 2013 11:29
Cálculo: Limites, Derivadas e Integrais
-
- Otimizacao
por Taisa » Sex Nov 12, 2010 13:53
- 1 Respostas
- 2142 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 14:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ) e então basta que você resolva o sistema
) e então basta que você resolva o sistema