
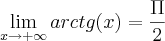
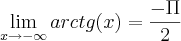
como eu acho esses limites da arctg de(x) e ,também onde eu coloco o resultado la na integral acima para chegar ao resultado de
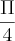
obrigado!
nessa integral aqui
 não consigo nem arrancar do inicio!
não consigo nem arrancar do inicio!

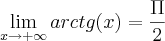
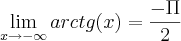
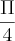
 não consigo nem arrancar do inicio!
não consigo nem arrancar do inicio!
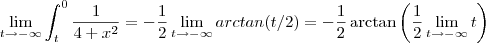 .
. 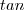 ,
, 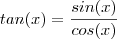 ;
; 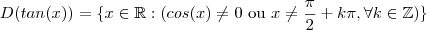 . Mas para obternos a função inversa da tangente vamos precisar trabalhar na imagem e domínio de forma que a função tangente seja injetora e sobrejetora. Assim ,vamos obter que a função tangente possui inversa
. Mas para obternos a função inversa da tangente vamos precisar trabalhar na imagem e domínio de forma que a função tangente seja injetora e sobrejetora. Assim ,vamos obter que a função tangente possui inversa  . Vamos fazer uma análise de forma obter a resposta do limite .
. Vamos fazer uma análise de forma obter a resposta do limite . 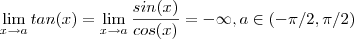 .O fato é que este resultado acima só ocorre quando
.O fato é que este resultado acima só ocorre quando  para
para  . Deste modo , temos :
. Deste modo , temos : 

 .Vamos dividir em duas etapas .
.Vamos dividir em duas etapas .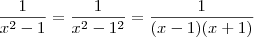 .
.  .
.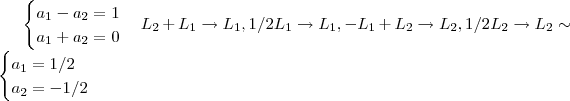

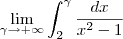 .
. ![\int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right ) \int _{2}^{\infty}\frac{dx}{x^2 - 1} = \frac{1}{2}\lim_{\gamma \to +\infty} \left(\int _{2}^{\gamma}\left[\frac{1}{x-1} - \frac{1}{x+1} \right] dx\right )](/latexrender/pictures/0a45ec7c8858f6622ad486046795e2cf.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)