Estou em dúvida de como prosseguir após chegar em uma determinada matriz. Segue o enunciado e até onde eu parei.
Sendo A=
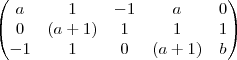 uma matriz ampliada de um sistema. Determinar os valores de a e b para que o sistema tenha infinitas soluções, uma solução e não tenha solução.
uma matriz ampliada de um sistema. Determinar os valores de a e b para que o sistema tenha infinitas soluções, uma solução e não tenha solução.Escalonei até:
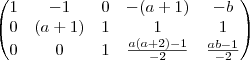
Não sei como concluir e se estou no caminho certo, alguma sugestão?
Agradeço desde já.


 e
e  .Mas lembre-se , quando temos uma linha inteira composta por zeros , vamos ter infinitas soluções .Para cada linha composta por zeros implica uma variável em função da outra . E quando não há solução , ocorre o seguinte
.Mas lembre-se , quando temos uma linha inteira composta por zeros , vamos ter infinitas soluções .Para cada linha composta por zeros implica uma variável em função da outra . E quando não há solução , ocorre o seguinte 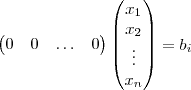 com
com 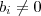 . E , é fácil ver que ,
. E , é fácil ver que , 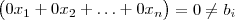 .
.

 .
.
 .
.

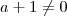
![([a+1]2)^{-1} L_2 \rightarrow L_2 \sim \begin{pmatrix} -1 &1 & 0 & a+1 & b \\ 0 & 1 & 0 & \frac{1 + a(a+2)}{2(a+1)} & \frac{1 + ba}{2(a+1)} \\ 0 &a+ 1 & - 1 & a(a+2) & ba\end{pmatrix} ([a+1]2)^{-1} L_2 \rightarrow L_2 \sim \begin{pmatrix} -1 &1 & 0 & a+1 & b \\ 0 & 1 & 0 & \frac{1 + a(a+2)}{2(a+1)} & \frac{1 + ba}{2(a+1)} \\ 0 &a+ 1 & - 1 & a(a+2) & ba\end{pmatrix}](/latexrender/pictures/efc007c8d4cbc89799a9e40fd2fd2678.png)

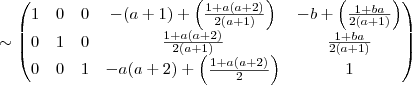
 o sistema não tem solução .(Verifique ! )
o sistema não tem solução .(Verifique ! )  ,
, 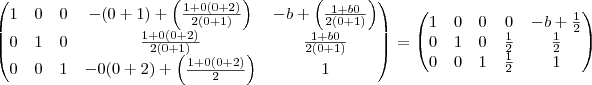
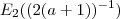 esta notação é o mesmo que
esta notação é o mesmo que 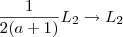 . Neste caso assumirmos
. Neste caso assumirmos 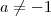 . Seu comentário foi importante , não necessariamente se
. Seu comentário foi importante , não necessariamente se  quer dizer que a o sistema linear não tem solução, o que acontece é que se
quer dizer que a o sistema linear não tem solução, o que acontece é que se  não existe a operação
não existe a operação  . A propósito , conseguiu concluir o exercício ? Existe um gabarito para este exercício ? Comente qualquer coisa .
. A propósito , conseguiu concluir o exercício ? Existe um gabarito para este exercício ? Comente qualquer coisa .