![\int_{}^{}\frac{dx}{2+2\sqrt[]{x}} \int_{}^{}\frac{dx}{2+2\sqrt[]{x}}](/latexrender/pictures/3955ebfd5f344094d5aa874b010f37a6.png)
Minhas contas:
![u=\sqrt[]{x}; \frac{du}{dx}=\frac{1}{2\sqrt[]{x}}; du=\frac{1}{2\sqrt[]{x}}dx; 2\sqrt[]{x}du=dx u=\sqrt[]{x}; \frac{du}{dx}=\frac{1}{2\sqrt[]{x}}; du=\frac{1}{2\sqrt[]{x}}dx; 2\sqrt[]{x}du=dx](/latexrender/pictures/7133a24906a69f8b4db283dc7059348f.png)


Cheguei até aí em cima, e não consegui desenvolver mais a conta, pois estão me faltando conhecimentos. Fui no Wolfram e ele me deu o seguinte resultado:

De onde saiu esse sinal de negativo no integrando? e pra onde fou o
 que estava no numerador?
que estava no numerador?
E depois parece que o Wolfram fez mais outra substuição:

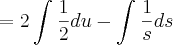
Aí fica fácil resolver, usando a tabela...
Poderiam me ajudar a entender essa substituição? Principalmente na parte em que aparece um sinal de negativo no integrando?










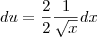
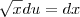
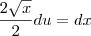
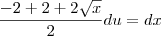
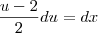
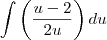
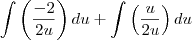
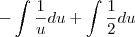
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)