Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como posso resolver isso????
por Mimizinha » Qui Mar 20, 2008 10:15
- 6 Respostas
- 6576 Exibições
- Última mensagem por Mimizinha

Qui Mar 20, 2008 13:15
Geometria Analítica
-
- Posso fazer isso?
por Cleyson007 » Qui Mai 03, 2012 09:54
- 5 Respostas
- 2595 Exibições
- Última mensagem por LuizAquino

Qui Mai 03, 2012 16:20
Cálculo: Limites, Derivadas e Integrais
-
- Como posso Identificar o domínio ?
por Amanda j » Seg Out 24, 2016 12:57
- 0 Respostas
- 3670 Exibições
- Última mensagem por Amanda j

Seg Out 24, 2016 12:57
Cálculo: Limites, Derivadas e Integrais
-
- Sem usar a fórmula de Herao como posso fazer
 por zenildo » Qui Jun 09, 2016 18:38
por zenildo » Qui Jun 09, 2016 18:38
- 1 Respostas
- 1954 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 11, 2016 09:07
Geometria Analítica
-
- como se faz isso
por Amandatkm » Dom Abr 28, 2013 17:50
- 1 Respostas
- 2787 Exibições
- Última mensagem por young_jedi

Seg Abr 29, 2013 12:42
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
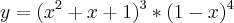
![y'=[3(x^2+x+1)^2*(2x+1)]*(1-x)^4+(x^2+x+1)^3*4(1-x)^3*(-1) y'=[3(x^2+x+1)^2*(2x+1)]*(1-x)^4+(x^2+x+1)^3*4(1-x)^3*(-1)](/latexrender/pictures/5ece83075844a93a8d3bcf2519fe795a.png)

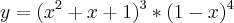
![y'=[3(x^2+x+1)^2*(2x+1)]*(1-x)^4+(x^2+x+1)^3*4(1-x)^3*(-1) y'=[3(x^2+x+1)^2*(2x+1)]*(1-x)^4+(x^2+x+1)^3*4(1-x)^3*(-1)](/latexrender/pictures/5ece83075844a93a8d3bcf2519fe795a.png)

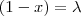 e
e  .Segue ,
.Segue , 
![y' = \psi^2 [(6x + 3)\cdot \lambda - 4\psi]\cdot \lambda ^3 y' = \psi^2 [(6x + 3)\cdot \lambda - 4\psi]\cdot \lambda ^3](/latexrender/pictures/99532e02ffa55cde8896121507232530.png)
![y' =(x^2 + x + 1)^2(1-x)^3[3(1 +x +1)(1-x) - 4(x^2 + x +1)] y' =(x^2 + x + 1)^2(1-x)^3[3(1 +x +1)(1-x) - 4(x^2 + x +1)]](/latexrender/pictures/a7899066d34a62f3603ee10a533d2573.png)
![y' = (x^2 + x + 1)^2(1-x)^3 [ 3(1 - x^2 +1 -x) -4x^2 - 4x -4 ] y' = (x^2 + x + 1)^2(1-x)^3 [ 3(1 - x^2 +1 -x) -4x^2 - 4x -4 ]](/latexrender/pictures/dec910583f4467fe4412e2ea5a0d4f0b.png)
![y' = (x^2 + x + 1)^2(1-x)^3[2 - 7x^2 - 7x] y' = (x^2 + x + 1)^2(1-x)^3[2 - 7x^2 - 7x]](/latexrender/pictures/381818049047a1fde9dd461fa20133fe.png) .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.