 por raimundoocjr » Dom Dez 16, 2012 18:14
por raimundoocjr » Dom Dez 16, 2012 18:14
01. (UEPA-2013) A Criatividade artística dos brasileiros é conhecida em todo o mundo, e algumas dessas
criações envolvem figuras geométricas como as circunferências ilustradas na figura abaixo. As circunferências
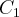
e

são concêntricas na origem, cujos diâmetros medem
d e
D, respectivamente. A equação da circunferência
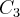
, em destaque, é:


Tentativa de Resolução;
Pensei que o raio fosse o indicado abaixo;

Porém, não é o que confere na alternativa proposta.
Gabarito Preliminar: C
-
raimundoocjr
-
 por raimundoocjr » Dom Dez 16, 2012 19:37
por raimundoocjr » Dom Dez 16, 2012 19:37
Obrigado. Pensando também que a diferença dos diâmetros é igual a quatro vezes o raio da circunferência menor seria uma boa opção (

). É só imaginar dividir o excedente de cima e de baixo em quatro partes. Fica aí a dica para os próximos.
-
raimundoocjr
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [perímetro; raio; sistema; Pitágoras] Geometria Plana
por claudia » Qua Ago 13, 2008 17:22
- 5 Respostas
- 8813 Exibições
- Última mensagem por claudia

Qui Ago 14, 2008 18:30
Geometria Plana
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7689 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5449 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4176 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3951 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
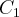 e
e  são concêntricas na origem, cujos diâmetros medem d e D, respectivamente. A equação da circunferência
são concêntricas na origem, cujos diâmetros medem d e D, respectivamente. A equação da circunferência 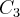 , em destaque, é:
, em destaque, é:



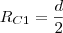
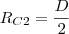
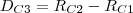
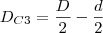
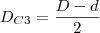
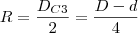
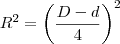

 ). É só imaginar dividir o excedente de cima e de baixo em quatro partes. Fica aí a dica para os próximos.
). É só imaginar dividir o excedente de cima e de baixo em quatro partes. Fica aí a dica para os próximos.