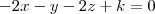por ricardosanto » Sex Dez 14, 2012 11:23
por ricardosanto » Sex Dez 14, 2012 11:23
Determinar a equação da reta que passa pelo pont A= (2 . -1, 1 ) e é perpendicular ao plano a: -2x - y -2z - 5 = 0
estou em duvida se ele quer a equação paramétrica (ou se só existe a paramétrica) desculpe minha ignorancia no assunto.
mas pelo que penso deve ser assim:
os parametros são -2 -1 -2 (vetor tirado do plano)
x= 2 + (-2) t
y= -1 + (-1)t
z= 1 + (-2) t
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por young_jedi » Sex Dez 14, 2012 12:10
por young_jedi » Sex Dez 14, 2012 12:10
seu pensamento esta correto realmente essas equações que voce colocou são as equações parametricas da reta
não existe só a equação parametrica, ela tambem pode ser escrita de forma diferente, por exemplo isolando o t em uma das equações e substituindo nas outras duas, mais não é necessario as equações parametricas ja são suficiente, a menos que seja exigido outra forma.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ricardosanto » Sex Dez 14, 2012 12:27
por ricardosanto » Sex Dez 14, 2012 12:27
young_jedi escreveu:seu pensamento esta correto realmente essas equações que voce colocou são as equações parametricas da reta
não existe só a equação parametrica, ela tambem pode ser escrita de forma diferente, por exemplo isolando o t em uma das equações e substituindo nas outras duas, mais não é necessario as equações parametricas ja são suficiente, a menos que seja exigido outra forma.
Haa cara vlw mesmo pela ajuda. Gostaria de saber tbm o que significa este valor -5 da equação, e pra que que ele serve.
Obrigado mesmo.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por young_jedi » Sex Dez 14, 2012 13:13
por young_jedi » Sex Dez 14, 2012 13:13
este -5 ele faz parte da equação do plano
se voce tomar o vetor (-2,-1,-2) este vetor é normal ao plano, mais não é normal somente a este plano mais a infinitos planos, sendo todos eles da forma
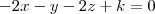
onde k pode ter infinitos valores, configurando assim infinitos planos diferentes sendo todos eles paraelelos enter si e normais ao vetor(-2,-1,-2)
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2460 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1592 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação da Reta
por aline2010 » Dom Jun 13, 2010 23:16
- 1 Respostas
- 1650 Exibições
- Última mensagem por Elcioschin

Seg Jun 14, 2010 12:16
Geometria Analítica
-
- Equação da reta
por marcio277 » Sex Nov 19, 2010 15:04
- 1 Respostas
- 1523 Exibições
- Última mensagem por Molina

Sex Nov 19, 2010 15:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.