Boa tarde...
Tenho a duvida da função abaixo, preciso saber como chegar nos pontos criticos (são 4, conforme mostrei abaixo):
Função:
f(x,y) = xy(1-x-y) = xy - x²y-xy²
derivando em x e y:
==> f[x] = y-2xy - y² = y(1-2x-y) = 0
e
==> f[y] = x-2xy - x² = x(1-x-2y) = 0
Resolvendo o sistema acima, temos os pontos criticos:
(i) (0,0)
{ii) (1,0)
(iii) (0,1)
(iv) (1/3, 1/3)
A questão é...como chegar até esses pontos? Obrigado desde já!


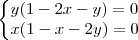
 é solução. Agora, tomando
é solução. Agora, tomando  e
e  não nulos podemos dividir a 1° equação por
não nulos podemos dividir a 1° equação por 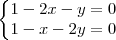
 , e aplicando na 2°, temos
, e aplicando na 2°, temos  .
. 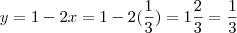 .
.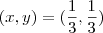 .
.