 por Leticiamed » Dom Dez 02, 2012 10:56
por Leticiamed » Dom Dez 02, 2012 10:56
Considere as funções f(y) = ?1-y², para y ? R, com -1?y?1 e g(x) = sen(2x), para x ? R. Resolva a equação (fog)(x) = 1/2.
Obs: Eu vi a resolução na minha apostila e me perdi nas passagens, estou completamente confusa.
-
Leticiamed
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Dez 02, 2012 10:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibular
- Andamento: formado
 por e8group » Dom Dez 02, 2012 19:54
por e8group » Dom Dez 02, 2012 19:54
Boa tarde .Por favor , sua função é definida por
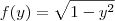
ou por
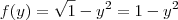
?
Eu acredito que seja a primeira , sendo assim .Veja que
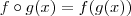
. Dada a função

,
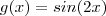
vamos ter
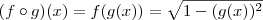
. Lembrando que ,
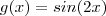
implica
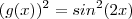
.Daí ,

. Pela identidade trigonométrica fundamental
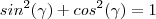
.Vamos concluir que ,

.
Basta achar os respectivos valores para

que
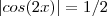
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Leticiamed » Seg Dez 03, 2012 13:19
por Leticiamed » Seg Dez 03, 2012 13:19
Ah, já perguntei para varias pessoas sobre esse exercício e ninguém consegue me explicar, mas obrigada de qualquer maneira
-
Leticiamed
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Dez 02, 2012 10:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibular
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questao. trigonometria.
por enraikou » Sex Fev 04, 2011 19:49
- 1 Respostas
- 1697 Exibições
- Última mensagem por enraikou

Sex Fev 04, 2011 21:09
Trigonometria
-
- Questão de Trigonometria
 por joaoxky » Sex Nov 18, 2011 00:01
por joaoxky » Sex Nov 18, 2011 00:01
- 2 Respostas
- 2233 Exibições
- Última mensagem por joaoxky

Sex Nov 18, 2011 12:07
Trigonometria
-
- Questão de Trigonometria II
por Leticiamed » Dom Dez 02, 2012 11:01
- 1 Respostas
- 2929 Exibições
- Última mensagem por DanielFerreira

Dom Dez 02, 2012 18:53
Trigonometria
-
- Questão trigonometria
por JovaniSouza » Ter Jul 29, 2014 17:52
- 0 Respostas
- 2154 Exibições
- Última mensagem por JovaniSouza

Ter Jul 29, 2014 17:52
Trigonometria
-
- Dúvida em questão de Trigonometria
por carlosvinnicius » Qui Fev 24, 2011 21:00
- 3 Respostas
- 3369 Exibições
- Última mensagem por yanagranhen

Ter Abr 02, 2013 21:09
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



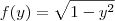 ou por
ou por 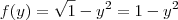 ?
? 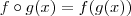 . Dada a função
. Dada a função  ,
, 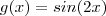 vamos ter
vamos ter 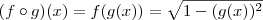 . Lembrando que ,
. Lembrando que , 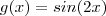 implica
implica 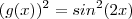 .Daí ,
.Daí ,  . Pela identidade trigonométrica fundamental
. Pela identidade trigonométrica fundamental 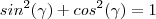 .Vamos concluir que ,
.Vamos concluir que ,  .
. que
que 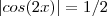 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.