![y=\sqrt[3]{x^2} y=\sqrt[3]{x^2}](/latexrender/pictures/4b63d449fe81825456b97639e662b5bb.png) +3
+3do ponto A(1,4) ao ponto B(8,7)
aqui derivei a função e encontrei
![f'(x)= \frac{2}{3\sqrt[3]{x}} f'(x)= \frac{2}{3\sqrt[3]{x}}](/latexrender/pictures/3ece75cc5af0c6d77040b1db212e2e21.png)
![L= \int_{1}^{8}\sqrt[2]{1+(\frac{2}{3\sqrt[3]{x}})^2}dx L= \int_{1}^{8}\sqrt[2]{1+(\frac{2}{3\sqrt[3]{x}})^2}dx](/latexrender/pictures/65cff9f675465acbd6751a3ac6612a1b.png)
fazendo as operações cheguei em:
![\frac{1}{3}\int_{1}^{8}\sqrt[2]{9+{4x}^{\frac{-2}{3}}dx} \frac{1}{3}\int_{1}^{8}\sqrt[2]{9+{4x}^{\frac{-2}{3}}dx}](/latexrender/pictures/3122dc58f9204c6b42b5d65087ac0068.png)
será que está correto? se está não consigo prosseguir, alguém me ajude ?

![y=\sqrt[3]{x^2} y=\sqrt[3]{x^2}](/latexrender/pictures/4b63d449fe81825456b97639e662b5bb.png) +3
+3![f'(x)= \frac{2}{3\sqrt[3]{x}} f'(x)= \frac{2}{3\sqrt[3]{x}}](/latexrender/pictures/3ece75cc5af0c6d77040b1db212e2e21.png)
![L= \int_{1}^{8}\sqrt[2]{1+(\frac{2}{3\sqrt[3]{x}})^2}dx L= \int_{1}^{8}\sqrt[2]{1+(\frac{2}{3\sqrt[3]{x}})^2}dx](/latexrender/pictures/65cff9f675465acbd6751a3ac6612a1b.png)
![\frac{1}{3}\int_{1}^{8}\sqrt[2]{9+{4x}^{\frac{-2}{3}}dx} \frac{1}{3}\int_{1}^{8}\sqrt[2]{9+{4x}^{\frac{-2}{3}}dx}](/latexrender/pictures/3122dc58f9204c6b42b5d65087ac0068.png)

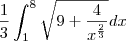
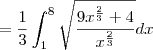
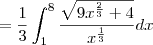
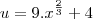
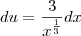
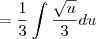

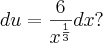

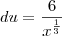
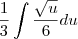


Crist escreveu:Terminei a questão e encontrei L= 7,62, obrigada pela ajuda, espero que meus cálculos estejam certos.

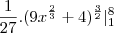
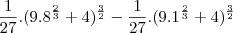
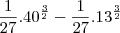
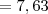

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)