2x1 + 2x2 + 2x3 = 0
-2X1+ 5x2+2x3 = 1
8x1 + x2 + 4x3 = -1
Bom, colocando o sistema na forma matricial, escalonando e colocando na forma reduzida... eu cheguei na seguinte matriz:

Bom, na verdade a matriz é 3x3, sendo a última linha sendo composta só por zeros.. mas eu não consegui representar usando o latex.
A resposta, segundo o livro é x1 = -1/7 - 3/7

x2 = 1/7 - 4/7

x3 =

Eu não entendi a resposta... (ela está na forma matricial, sendo x1, x2, x3 representando uma coluna e cada linha o outro lado da igualdade...)
na última linha fica apenas 0 0 0 0... por que isso vai ser igual a
 ?????? Grato desde já!
?????? Grato desde já!

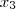 assumir implicará uma solução verdadeira que satisfaz cada equação ,isto é, para cada valor que
assumir implicará uma solução verdadeira que satisfaz cada equação ,isto é, para cada valor que 

 .
.
 :
: