 por Danilo » Qua Nov 28, 2012 20:08
por Danilo » Qua Nov 28, 2012 20:08
Resolver o sistema utilizando o método de Gauss-Jordan
2x1 + 2x2 + 2x3 = 0
-2X1+ 5x2+2x3 = 1
8x1 + x2 + 4x3 = -1
Bom, colocando o sistema na forma matricial, escalonando e colocando na forma reduzida... eu cheguei na seguinte matriz:

Bom, na verdade a matriz é 3x3, sendo a última linha sendo composta só por zeros.. mas eu não consegui representar usando o latex.
A resposta, segundo o livro é x1 = -1/7 - 3/7

x2 = 1/7 - 4/7

x3 =

Eu não entendi a resposta... (ela está na forma matricial, sendo x1, x2, x3 representando uma coluna e cada linha o outro lado da igualdade...)
na última linha fica apenas 0 0 0 0... por que isso vai ser igual a

?????? Grato desde já!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qua Nov 28, 2012 20:42
por e8group » Qua Nov 28, 2012 20:42
A última linha é composta por zeros certo ? Se isto for verdade, quer dizer que para quaisquer valores que
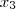
assumir implicará uma solução verdadeira que satisfaz cada equação ,isto é, para cada valor que

assumir temos uma nova solução ,infintas soluções . Para compreender isto , note que inicialmente temos uma matriz
 ( 3 equações e 3 incógnitas )
( 3 equações e 3 incógnitas ) .Mas, após operações elementares , obtemos
2 equações para 3 incógnitas ,como o número de equações é menor que o de variáveis ,há de esperar que teremos uma incógnita em função da outra .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Método de Gauss Jordan
por Claudin » Sex Ago 26, 2011 03:00
- 2 Respostas
- 4782 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 22:51
Álgebra Elementar
-
- Método de de Gauss-Jordan
por AmandaPmend » Seg Nov 10, 2014 14:46
- 1 Respostas
- 3530 Exibições
- Última mensagem por adauto martins

Ter Nov 11, 2014 14:51
Álgebra Linear
-
- Metodo de Gauss Jordan em Matriz 4x4 (Dificil)
por Rhyu » Sex Abr 06, 2012 17:26
- 1 Respostas
- 18511 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 21:31
Matrizes e Determinantes
-
- Como aplicar o metodo de Gauss Jordan nesse sistema.
por 380625 » Sáb Ago 20, 2011 16:19
- 3 Respostas
- 6084 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 22:26
Sistemas de Equações
-
- [Sistemas Lineares] Precisão do Método de Gauss-Seidel
por VFernandes » Qui Out 06, 2011 13:50
- 0 Respostas
- 1116 Exibições
- Última mensagem por VFernandes

Qui Out 06, 2011 13:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ?????? Grato desde já!
?????? Grato desde já!

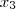 assumir implicará uma solução verdadeira que satisfaz cada equação ,isto é, para cada valor que
assumir implicará uma solução verdadeira que satisfaz cada equação ,isto é, para cada valor que 