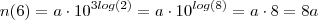por karen » Ter Nov 27, 2012 20:01
por karen » Ter Nov 27, 2012 20:01
Uma cultura de bactérias cresce segundo a lei
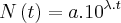
, onde N(t) é o número de bactérias em t horas,

, e a e

são constantes estritamente positivas. Se após 2 horas o número inicial de bactérias, N(0), é duplicado, após 6horas o número de bactérias será:
Primeiro eu fiz
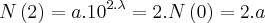
e cheguei em
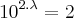
Não sei continuar...
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por e8group » Ter Nov 27, 2012 20:13
por e8group » Ter Nov 27, 2012 20:13
Aplique logaritmo em ambos lados . Vamos ter ,

.Agora tente concluir o exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por karen » Ter Nov 27, 2012 20:31
por karen » Ter Nov 27, 2012 20:31
Continuando...
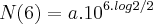
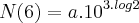
E agora?
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por e8group » Ter Nov 27, 2012 20:43
por e8group » Ter Nov 27, 2012 20:43

Por definição ,
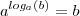
.É fácil ver que ,

aplicando a definição de logaritmo
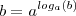
. Daí ,
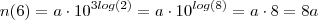
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por karen » Ter Nov 27, 2012 20:47
por karen » Ter Nov 27, 2012 20:47
bacana, vou dar uma revisada nessas propriedades....
Obrigadão!
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UNESP
por Guilherme Carvalho » Sex Mai 13, 2011 14:08
- 1 Respostas
- 11377 Exibições
- Última mensagem por carlosalesouza

Sex Mai 13, 2011 17:04
Trigonometria
-
- Unesp - 95 Números Complexos
por Alucard014 » Dom Ago 01, 2010 18:22
- 1 Respostas
- 51901 Exibições
- Última mensagem por MarceloFantini

Qui Ago 05, 2010 17:27
Números Complexos
-
- (UNESP)BINÔMIO DE NEWTON
por natanskt » Sex Dez 10, 2010 21:27
- 2 Respostas
- 6356 Exibições
- Última mensagem por natanskt

Sex Dez 10, 2010 22:38
Binômio de Newton
-
- [números complexos] UNESP
por JKS » Dom Set 23, 2012 01:31
- 1 Respostas
- 3315 Exibições
- Última mensagem por MarceloFantini

Dom Set 23, 2012 01:58
Números Complexos
-
- (UNESP-SP) SISTEMA LINEAR
por lnd_rj1 » Dom Fev 10, 2013 09:06
- 1 Respostas
- 1066 Exibições
- Última mensagem por DanielFerreira

Dom Fev 10, 2013 21:20
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
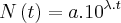 , onde N(t) é o número de bactérias em t horas,
, onde N(t) é o número de bactérias em t horas,  , e a e
, e a e  são constantes estritamente positivas. Se após 2 horas o número inicial de bactérias, N(0), é duplicado, após 6horas o número de bactérias será:
são constantes estritamente positivas. Se após 2 horas o número inicial de bactérias, N(0), é duplicado, após 6horas o número de bactérias será: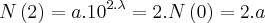
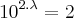


 .Agora tente concluir o exercício .
.Agora tente concluir o exercício .
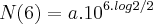
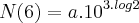

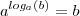 .É fácil ver que ,
.É fácil ver que ,  aplicando a definição de logaritmo
aplicando a definição de logaritmo 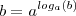 . Daí ,
. Daí ,