48) O valor de uma série uniforme A, um tempo antes do 1º pagamento, onde se tem n pagamentos iguais a P, e i é a taxa de juros, é obtido pela soma mostrada abaixo:
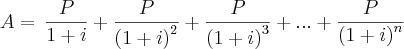
Uma forma equivalente dessa série é dada por:
a)
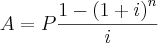
b)
 (resposta certa)
(resposta certa)c)
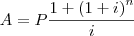
d)
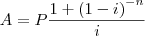
e)
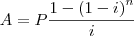
Eu tentei fazer tipo racionalizar, multipliquei o numerador e o denominador por
 e não cheguei a nenhum lugar. Aguém tem uma ideia?
e não cheguei a nenhum lugar. Aguém tem uma ideia?

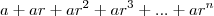

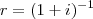
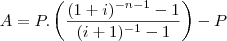

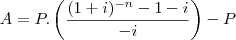


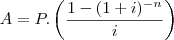

 .
.
 :
: