[CURVAS] Gráfico da função, ponto mais próximo de um plano

por **inkz** » Qui Nov 22, 2012 02:49

UM PONTO P DESCREVE UMA CURVA SOBRE O GRÁFICO DA FUNÇÃO f(x,y) = x² + y² DE MODO QUE SUA PROJEÇÃO Q SOBRE O PLANO xy DESCREVE A RETA x + y = 1. DETERMINE O PONTO DA CURVA QUE SE ENCONTRA MAIS PRÓXIMO DO PLANO xy.

Não consegui nem entender o enunciado galera.. alguém pode me dar uma ajuda sobre o que devo fazer?
abraços!!

por **LuizAquino** » Qui Nov 22, 2012 11:12

inkz escreveu:UM PONTO P DESCREVE UMA CURVA SOBRE O GRÁFICO DA FUNÇÃO f(x,y) = x² + y² DE MODO QUE SUA PROJEÇÃO Q SOBRE O PLANO xy DESCREVE A RETA x + y = 1. DETERMINE O PONTO DA CURVA QUE SE ENCONTRA MAIS PRÓXIMO DO PLANO xy.

Não consegui nem entender o enunciado galera.. alguém pode me dar uma ajuda sobre o que devo fazer?
abraços!!

A figura abaixo ilustra o exercício.

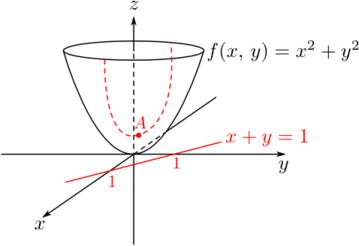
: figura.png (13.61 KiB) Exibido 4404 vezes

Note que o gráfico da função f é um paraboloide. Além disso, note que a curva descrita pela trajetória do ponto P (linha pontilhada em vermelho) sobre o gráfico de f forma uma parábola. O objetivo do exercício é determinar o ponto A, que representa o ponto dessa curva que está mais próximo do plano xy.

Para determinar o ponto A, comece observando que como ele está sobre o gráfico de f ele tem coordenadas (x, y, x² + y²), para algum par de números x e y.

Por outro lado, como a projeção de A está sobre a reta x + y = 1 (ou seja, y = 1 - x), podemos reescrever suas coordenadas como (x, 1 - x, x² + (1 - x)²).

Tudo que você precisa fazer agora é determinar qual é o valor de x que faz o ponto A ficar mais próximo do plano xy. Em outras palavras, você precisa determinar qual é o valor de x para o qual a distância do ponto A até o plano xy é a menor possível.

Agora tente concluir o exercício a partir daí.