 por Aprendiz2012 » Qui Nov 22, 2012 15:15
por Aprendiz2012 » Qui Nov 22, 2012 15:15
5) Considerando

use manipulações algébricas e escreva a série de potências que representa a função

"manipulações algébricas" seria eu trocar os valores??
resposta:
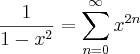
-
Aprendiz2012
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sáb Ago 11, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em química
- Andamento: formado
 por MarceloFantini » Qui Nov 22, 2012 17:46
por MarceloFantini » Qui Nov 22, 2012 17:46
Sim, está correto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qui Nov 22, 2012 19:27
por e8group » Qui Nov 22, 2012 19:27
Pensei assim,
Se
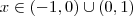
é verdade que ,

.Tome por exemplo -3 e 2 . Faça o teste .
Já ,

caso assumirmos

, temos que
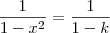
.
Ora , para quaisquer valores que

assumir,
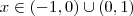
vamos ter,
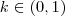
.
Portanto ,
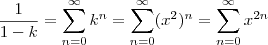
.
O que acha ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Nov 22, 2012 19:54
por MarceloFantini » Qui Nov 22, 2012 19:54
A série é convergente para

também. A restrição é apenas que

, e no caso que

também.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Séries] Sobre simplicação de expressões em séries
por HenriqueOrlan » Sáb Nov 21, 2015 11:28
- 1 Respostas
- 3727 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:31
Sequências
-
- derivada meio dificil duvidas
 por giboia90 » Sex Dez 23, 2011 23:20
por giboia90 » Sex Dez 23, 2011 23:20
- 6 Respostas
- 3633 Exibições
- Última mensagem por LuizAquino

Dom Fev 19, 2012 08:45
Cálculo: Limites, Derivadas e Integrais
-
- Determinante de Matriz por Meio de Triangulação
por elisafrombrazil » Dom Jan 29, 2017 20:59
- 1 Respostas
- 15350 Exibições
- Última mensagem por petras

Seg Jan 30, 2017 19:11
Álgebra Linear
-
- Séries
por Guilherme Carvalho » Seg Set 17, 2012 22:50
- 5 Respostas
- 3450 Exibições
- Última mensagem por Guilherme Carvalho

Ter Set 18, 2012 16:24
Sequências
-
- Séries
por manuoliveira » Sex Mai 23, 2014 21:07
- 2 Respostas
- 2190 Exibições
- Última mensagem por Man Utd

Ter Mai 27, 2014 15:10
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 use manipulações algébricas e escreva a série de potências que representa a função
use manipulações algébricas e escreva a série de potências que representa a função 
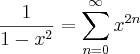

 use manipulações algébricas e escreva a série de potências que representa a função
use manipulações algébricas e escreva a série de potências que representa a função 
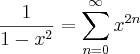


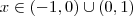 é verdade que ,
é verdade que ,  .Tome por exemplo -3 e 2 . Faça o teste .
.Tome por exemplo -3 e 2 . Faça o teste . 
 , temos que
, temos que 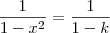 .
. assumir,
assumir, 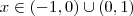 vamos ter,
vamos ter, 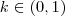 .
. 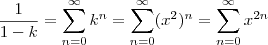 .
. 
 também. A restrição é apenas que
também. A restrição é apenas que  , e no caso que
, e no caso que  também.
também.
