alguem me pode explicar porque a interpretaçao geometrica do modulo de x<0 é o conjunto vazio enquanto o modulo de x>0 é R\{0}?
por favor



 quando
quando 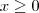 e
e 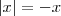 quando
quando 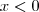 .
. não vamos encontrar um número real que torne essa expressão verdadeira, logo o conjunto-solução é o conjunto vazio.
não vamos encontrar um número real que torne essa expressão verdadeira, logo o conjunto-solução é o conjunto vazio. vamos encontrar todos os reais, exceto o número 0 como solução.
vamos encontrar todos os reais, exceto o número 0 como solução.
 ) ou a distância entre dois pontos no geral (quando escrevemos
) ou a distância entre dois pontos no geral (quando escrevemos  , coincidindo quando
, coincidindo quando  ).
).

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: