 por rodrigonapoleao » Seg Nov 19, 2012 14:37
por rodrigonapoleao » Seg Nov 19, 2012 14:37
alguem me pode explicar porque a interpretaçao geometrica do modulo de x<0 é o conjunto vazio enquanto o modulo de x>0 é R\{0}?
por favor
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por fraol » Seg Nov 19, 2012 21:25
por fraol » Seg Nov 19, 2012 21:25
Olá, boa noite.
O módulo de um número real, por definição é um número positivo ou nulo.
Revendo a definição:

quando
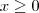
e
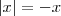
quando
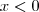
.
Dessa forma analisando as duas expressões que você postou, iremos concluir que para:

não vamos encontrar um número real que torne essa expressão verdadeira, logo o conjunto-solução é o conjunto vazio.

vamos encontrar todos os reais, exceto o número 0 como solução.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Seg Nov 19, 2012 22:56
por MarceloFantini » Seg Nov 19, 2012 22:56
A interpretação geométrica do módulo é sempre a distância de um ponto até a origem (no caso

) ou a distância entre dois pontos no geral (quando escrevemos

, coincidindo quando

).
Note que da forma como está definido, distância é sempre maior ou igual a zero. Logo, o conjunto dos pontos que está a uma distância negativa da origem é vazio, pois não existem pontos cuja distância até a origem seja negativa.
Da mesma forma, o conjunto dos pontos cuja distância até a origem é maior que zero é o conjunto de todos os números reais diferentes de zero, pois a distância de zero a ele mesmo é zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- porque o trigonometria
por antonybel » Sex Nov 11, 2011 13:16
- 1 Respostas
- 2465 Exibições
- Última mensagem por Neperiano

Sex Nov 11, 2011 14:01
Piadas
-
- O porque disso.
por Bielto » Qui Jul 26, 2012 10:38
- 6 Respostas
- 2947 Exibições
- Última mensagem por Claudin

Qui Jul 26, 2012 18:54
Álgebra Elementar
-
- Porque a base {1, x, x², ..., x^n} define Pn?
por Hiperbanka » Qui Jul 02, 2009 22:22
- 1 Respostas
- 2193 Exibições
- Última mensagem por Fred33

Sáb Jul 11, 2009 09:00
Álgebra Linear
-
- [Duvida]Respostas diferentes e equivalentes, porque?
por Deivid » Ter Set 21, 2010 18:07
- 2 Respostas
- 1933 Exibições
- Última mensagem por Deivid

Qua Set 22, 2010 14:29
Cálculo: Limites, Derivadas e Integrais
-
- o porquê de aprender vetores em Geometria Analítica
por hadnet » Sáb Jan 26, 2013 19:26
- 4 Respostas
- 4141 Exibições
- Última mensagem por hadnet

Seg Jan 28, 2013 23:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 quando
quando 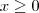 e
e 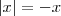 quando
quando 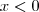 .
. não vamos encontrar um número real que torne essa expressão verdadeira, logo o conjunto-solução é o conjunto vazio.
não vamos encontrar um número real que torne essa expressão verdadeira, logo o conjunto-solução é o conjunto vazio. vamos encontrar todos os reais, exceto o número 0 como solução.
vamos encontrar todos os reais, exceto o número 0 como solução.
 ) ou a distância entre dois pontos no geral (quando escrevemos
) ou a distância entre dois pontos no geral (quando escrevemos  , coincidindo quando
, coincidindo quando  ).
).
