 por JU201015 » Seg Nov 19, 2012 00:36
por JU201015 » Seg Nov 19, 2012 00:36
(UFRGS) Considere esta progressão geométrica:
3 ; 0,3 ; 0,03 ; 0,003 ; ...
Os logaritmos decimais de cada um destes números, na ordem em que estão dispostos, formam uma:
a) progressão geométrica de razão 0,01.
b) progressão geométrica de razão 0,1;
c) progressão aritmética de razão 0,1.
d) progressão aritmética de razão -1.
e) progressão geométrica de razão -1.
Não sei como analisar a diferença entre os logaritmos. Me ajudem?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Nov 19, 2012 09:22
por e8group » Seg Nov 19, 2012 09:22
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por replay » Seg Nov 19, 2012 11:41
por replay » Seg Nov 19, 2012 11:41
Desculpe interferir no tópico que nem é meu.
Mas eu acho que nem precisaria de calculo, é que parece que fica meio óbvio que é 0,1.
Mas a duvida é: O exercicio espera que o aluno saiba reconhecer uma PA ou PG ? Seria isso ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 12:45
por MarceloFantini » Seg Nov 19, 2012 12:45
Ju escreveu:(UFRGS) Considere esta progressão geométrica:
3 ; 0,3 ; 0,03 ; 0,003 ; ...
Os logaritmos decimais de cada um destes números, na ordem em que estão dispostos
Nós já temos uma progressão geométrica dada por

. Ele quer que consideremos os
logaritmos decimais, logo devemos tomar
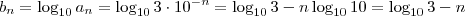
.
Façamos a diferença entre dois termos consecutivos:
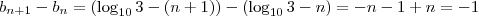
,
portanto é uma progressão aritmética de razão -1[/tex].
Note que é fácil errar estando desatento, pois ele dá uma sequência e depois diz "[...] números, na ordem em que estão dispostos, formam uma" e nisso marcam progressão geométrica de razão 0,1.
Replay, fique a vontade. Todos estão encorajados a contribuir positivamente nas discussões.

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Seg Nov 19, 2012 13:11
por JU201015 » Seg Nov 19, 2012 13:11
MarceloFantini escreveu:Ju escreveu:(UFRGS) Considere esta progressão geométrica:
3 ; 0,3 ; 0,03 ; 0,003 ; ...
Os logaritmos decimais de cada um destes números, na ordem em que estão dispostos
Nós já temos uma progressão geométrica dada por

. Ele quer que consideremos os
logaritmos decimais, logo devemos tomar
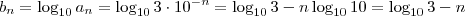
.
Façamos a diferença entre dois termos consecutivos:
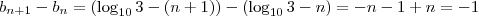
,
portanto é uma progressão aritmética de razão -1[/tex].
Note que é fácil errar estando desatento, pois ele dá uma sequência e depois diz "[...] números, na ordem em que estão dispostos, formam uma" e nisso marcam progressão geométrica de razão 0,1.
Replay, fique a vontade. Todos estão encorajados a contribuir positivamente nas discussões.

Muito obrigada MarceloFantini!! Até que enfim alguém respondeu de acordo com o gabarito kkk Mas ainda tenho uma duvidazinha rsrs Bom, quando chega em "-n -1 +n= -1", como vc chega a conclusão de que é uma PA de razão -1? Eu não consegui enxergar isso.
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 13:29
por MarceloFantini » Seg Nov 19, 2012 13:29
A definição de progressão aritmética é que a diferença entre dois termos consecutivos é constante. Seguindo isso, tomei dois termos consecutivos e calculei sua diferença, que se mostrou constante. Portanto é uma progressão aritmética.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Seg Nov 19, 2012 14:03
por JU201015 » Seg Nov 19, 2012 14:03
MarceloFantini escreveu:A definição de progressão aritmética é que a diferença entre dois termos consecutivos é constante. Seguindo isso, tomei dois termos consecutivos e calculei sua diferença, que se mostrou constante. Portanto é uma progressão aritmética.
Muitíssimo obrigada^^
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Seg Nov 19, 2012 14:09
por Cleyson007 » Seg Nov 19, 2012 14:09
P.A. --> {x1, x2, x3} --> Razão: x2 - x1 = x3 - x2
P.G --> {x1, x2, x3} --> Razão: x3/x2 = x2/x1
Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por e8group » Seg Nov 19, 2012 19:53
por e8group » Seg Nov 19, 2012 19:53
obrigado por responder . Não observei que tinha P.A de razão - 1 , nas alternativas , pensei q fosse P.G razão - 1 que estaria erado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4253 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4726 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25547 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4236 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2890 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



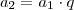
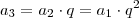

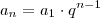

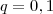

 . Ele quer que consideremos os
. Ele quer que consideremos os 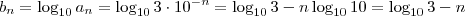 .
.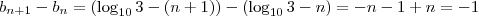 ,
,


