 por JU201015 » Sáb Nov 17, 2012 10:21
por JU201015 » Sáb Nov 17, 2012 10:21
As medidas dos lados de um retângulo e sua diagonal formam, nessa ordem, uma PA. Sabendo=se que o perímetro desse retângulo é igual a 14, determine a área desse retângulo.
Questão muito simples mas não sei fazer uma conta com os lados e diagonais formando uma PA. Me ajudem?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Sáb Nov 17, 2012 11:21
por Cleyson007 » Sáb Nov 17, 2012 11:21
JU201015, vou te dar as dicas. Ok?
As medidas dos lados do retângulo, são: x e y
2x + 2y = 14 (I)
Diagonal --> d² = x² + y²
P.A. = (x, y, Vx²+y²)
y - x = Vx²+y² - y (II) (Obs.: O V é raiz quadrada)
Basta resolver o sistema de equações, e encontrar os valores de x e y.
A área procurada é dada por A
r = x.y
Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Sáb Nov 17, 2012 11:29
por MarceloFantini » Sáb Nov 17, 2012 11:29
Sejam

e

os lados do retângulo e

sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que
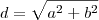
.
Pela definição de perímetro temos que
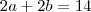
ou

.
Pela definição de progressão aritmética sabemos que a razão entre dois termos consecutivos é constante, logo

.
Substituindo

e
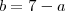
segue que

.
Simplificando,
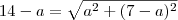
.
Tente terminar.

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Dom Nov 18, 2012 10:52
por JU201015 » Dom Nov 18, 2012 10:52
MarceloFantini escreveu:Sejam

e

os lados do retângulo e

sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que
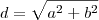
.
Pela definição de perímetro temos que
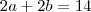
ou

.
Pela definição de progressão aritmética sabemos que a razão entre dois termos consecutivos é constante, logo

.
Substituindo

e
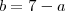
segue que

.
Simplificando,
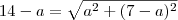
.
Tente terminar.

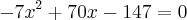
Encontro as raízes 7 e 3. Mas se x for 7, y será 0, então x é 3. Sendo x igual a 3, a PA fica:
PA=(X,Y,VX²+Y²)
PA=(3,4,5).
Logo, a área do retângulo é x.y=3.4=12.
Está correto?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Nov 18, 2012 23:41
por MarceloFantini » Dom Nov 18, 2012 23:41
Existe um erro na minha resolução, simplifiquei errado. A conta correta é
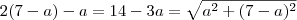
.
Resolvendo isto você encontrará

, daí

e

.
Como você encontrou a equação
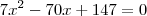
?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Seg Nov 19, 2012 12:30
por JU201015 » Seg Nov 19, 2012 12:30
MarceloFantini escreveu:Existe um erro na minha resolução, simplifiquei errado. A conta correta é
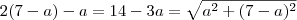
.
Resolvendo isto você encontrará

, daí

e

.
Como você encontrou a equação
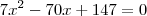
?
Eu simplifiquei diferente:
![\sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x \sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x](/latexrender/pictures/275e9d5d842fecef10f122d6c590af37.png)
Mas eu acertei do mesmo jeito =D
Obrigada^^
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6135 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4726 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5630 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4423 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8399 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 e
e  os lados do retângulo e
os lados do retângulo e  sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que
sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que 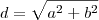 .
.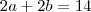 ou
ou  .
. .
. e
e 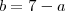 segue que
segue que .
.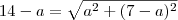 .
.

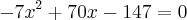
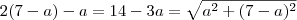 .
. , daí
, daí  e
e  .
.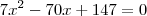 ?
?![\sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x \sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x](/latexrender/pictures/275e9d5d842fecef10f122d6c590af37.png)