Estava tentando resolver este exercício de trigonometria e sinceramente não consegui.Segue:
Determine, no ciclo trigonométrico, a distância entre os pontos correspondentes aos números dados:
 e
e 
O que eu fiz:
Transformei estas medidas angulares de radianos para graus (para ter uma noção do posicionamento no ciclo trigonométrico)
 =150°
=150° =210°
=210°Então diminuí 210° de 150° (a fim de verificar qual o arco formado entre eles)=60° em rad=

Então, como
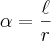 , e como quando, um arco está contido em uma circunferência cujo raio vale 1 (ciclo trigonométrico) o comprimento do arco é igual ao ângulo central correspondente
, e como quando, um arco está contido em uma circunferência cujo raio vale 1 (ciclo trigonométrico) o comprimento do arco é igual ao ângulo central correspondente  ...Cheguei a resposta igual a 1.0471.
...Cheguei a resposta igual a 1.0471.Mas segundo o livro é 1 a resposta.
Há outros exercícios também:
 e
e 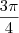
 e
e 


 e
e 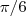 vale 30º e
vale 30º e  vale 210º
vale 210º vale 45º e
vale 45º e 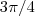 vale 135º
vale 135º



 , avisa que eu resolvo.
, avisa que eu resolvo.

