

Me ajudem? Não sei nem logaritmo direito quanto mais logaritmo em um sistema. Por favor.




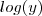 ou
ou  , depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .  , na primeira equação :
, na primeira equação : 

santhiago escreveu:isole ,ou
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
EX:
Somando, na primeira equação :

Agora substitua na segunda equação .
Consegue terminar ?

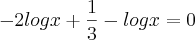
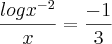

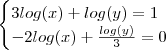 .
.  . Susbstituindo na segunda equação ,
. Susbstituindo na segunda equação ,  .
.  ,
, 
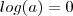 quando
quando 
![log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10} log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10}](/latexrender/pictures/793a82e214f7f9044b6b1ed66187a874.png) .
.  , isole
, isole  da relação
da relação  , susbstitua em
, susbstitua em  . Faça a mesma análise e resolva p/ y .
. Faça a mesma análise e resolva p/ y . 
santhiago escreveu:.
No tópico , acima , vimos que. Susbstituindo na segunda equação ,
.
Multiplicando toda equação por,

Sabemos quequando

Com isso ,.
Para resolver para, isole
da relação
, susbstitua em
. Faça a mesma análise e resolva p/ y .
Por favor revise seus cálculos .

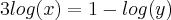
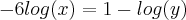
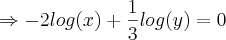
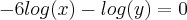
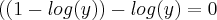



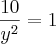

![y=\sqrt[]{10} y=\sqrt[]{10}](/latexrender/pictures/d0222f9916cde01009d3db653d22c32a.png)


 que voltará para a equação original .
que voltará para a equação original . 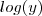 em função de
em função de  , lembrando
, lembrando 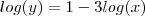 ( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos  ( Observe minha 2ª resposta ao tópico ) .
( Observe minha 2ª resposta ao tópico ) . 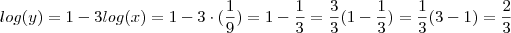 .
. 
![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)

santhiago escreveu:Cuidado ! você cometeu um erro grave que estar alterando o resultado .
Veja o certo ,
Multiplicando ambos lados da igualdade por - 2 .
Vamos obter ,
Perceba que , basta multiplicar pelo seu inverso , que vamos desfazer a operação anterior , isto é , multiplique toda toda equação porque voltará para a equação original .
Observe o seu desenvolvimento e faça uma comparação .
Mas , como já temosem função de
, lembrando
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
( Observe minha 2ª resposta ao tópico ) .
Sendo assim ,.
Daí ,
e
Portanto ,![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)
Qualquer coisa comente .

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)