Jhenrique escreveu:A interpretação para a razão entre duas grandezas é a de "
taxa de variação", que, para mim, é uma interpretação muito abrangente e excelente! Mas o que eu não entendo é o produto entre duas grandezas que geralmente é explicado como a área da
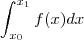
, tal explicação faz sentido para mim quando as grandezas

e

são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!
Considere os dois problemas abaixo.
Problema 1) Duas pessoas possuem cada uma 5 balas. Quantas balas elas possuem juntas?
Problema 2) Um retângulo possui lados medindo 2 cm e 5 cm. Qual é a área desse retângulo?
É fácil obter que a reposta desses problemas são, respectivamente, 10 balas e 10 cm².
Obviamente a grandeza "bala" é diferente da grandeza "cm²". Entretanto, em ambos os problemas a reposta é algo como: 10 unidades de "grandeza", onde a palavra "grandeza" pode ser substituída por "bala" ou por "cm²" conforme o caso. Nesse sentido, podemos afirmar que: encontrar a quantidade da grandeza no problema 1 é equivalente a encontrar a quantidade da grandeza no problema 2.
Podemos transpor essa ideia para o caso da integral que você citou. Suponha que a grandeza A é definida como o produto entre as grandezas B e C, isto é, por definição temos A = BC. Suponha ainda que certa função f contínua (e positiva) associa a grandeza B com a grandeza C. Desse modo, achar a quantidade da grandeza A quando a grandeza B varia no intervalo
![[b_0,\, b_1] [b_0,\, b_1]](/latexrender/pictures/1889e92cc0c025726fcda51918aae93a.png)
e a grandeza C varia conforme f no intervalo
![[f(b_0),\,f(b_1)] [f(b_0),\,f(b_1)]](/latexrender/pictures/5e0606543d5374f2647692cae88c76f5.png)
(ou
![[f(b_1),\,f(b_0)] [f(b_1),\,f(b_0)]](/latexrender/pictures/70a68dd7f9e97806ad5c0fc6ce79681d.png)
, caso

), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral

.
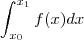 , tal explicação faz sentido para mim quando as grandezas
, tal explicação faz sentido para mim quando as grandezas  e
e  são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!
são comprimentos, mas nem sempre são comprimentos, podem ser qualquer outra grandeza, daí a interpretação da área, para mim, não é mais intuitiva. Portanto, como eu poderia interpretar conceitualmente o produto entre duas grandezas? Qualquer dica tá valendo!

![[b_0,\, b_1] [b_0,\, b_1]](/latexrender/pictures/1889e92cc0c025726fcda51918aae93a.png) e a grandeza C varia conforme f no intervalo
e a grandeza C varia conforme f no intervalo ![[f(b_0),\,f(b_1)] [f(b_0),\,f(b_1)]](/latexrender/pictures/5e0606543d5374f2647692cae88c76f5.png) (ou
(ou ![[f(b_1),\,f(b_0)] [f(b_1),\,f(b_0)]](/latexrender/pictures/70a68dd7f9e97806ad5c0fc6ce79681d.png) , caso
, caso  ), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral
), é equivalente a achar a quantidade da grandeza área que está abaixo do gráfico de f e acima do eixo x no intervalo dado para B. Essa quantidade de área é representada pela integral  .
.
 e
e  , respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz
, respectivamente. E isso não faz sentido para mim, como pode uma grandeza do tipo comprimento ser quadridimensional? Ou outra que não tem nada a ver com volume ser tridimensional? Outra vezes preciso extrair a raiz ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.