 por joedsonazevedo » Qui Nov 15, 2012 11:11
por joedsonazevedo » Qui Nov 15, 2012 11:11
Olá, estou para resolver essa questão que quer saber a área do trapézio
inscrito no gráfico através de uma função... me ajudem.. eu só consigo
fazer uma coisa de cada vez... não sei literalmente por onde começar...
Postei a imagem do gráfico e a questão na internet... por favor me ajudem...
 http://imageshack.us/photo/my-images/443/funo.jpg
http://imageshack.us/photo/my-images/443/funo.jpgMuito Obrigado;;; ;]
-
joedsonazevedo
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 08, 2012 14:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. em Informática
- Andamento: formado
 por e8group » Qui Nov 15, 2012 14:07
por e8group » Qui Nov 15, 2012 14:07
Por favor , na próxima vez digite o enunciado e se precisar anexar imagens , que de preferência seja aqui . Isto é possível neste fórum .
Quanto o enunciado perceba que ,
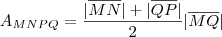
Temos os pontos que de interceptam o eixo x , são eles
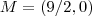
e

.
Já os pontos

pertencentes ao gráfico
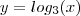
terão coordenadas ,
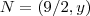
e

.
Para achar

quando
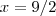
, basta resolver

, para o outro ponto o processo é análogo .
Com isso , tens a área do trapézio .
Comente aí qualquer coisa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular perímetro do quadrado] através da área do triângulo
 por lukasmetal » Qua Nov 30, 2011 12:11
por lukasmetal » Qua Nov 30, 2011 12:11
- 3 Respostas
- 3845 Exibições
- Última mensagem por lukasmetal

Qui Dez 01, 2011 12:19
Geometria Plana
-
- calcular a área da funçao
 por edilaine33 » Dom Dez 01, 2013 08:54
por edilaine33 » Dom Dez 01, 2013 08:54
- 1 Respostas
- 1695 Exibições
- Última mensagem por Pessoa Estranha

Dom Dez 01, 2013 10:13
Cálculo: Limites, Derivadas e Integrais
-
- Calcular primitiva atraves do metodo se substituiçao
por rodrigonapoleao » Seg Dez 17, 2012 17:25
- 1 Respostas
- 1609 Exibições
- Última mensagem por e8group

Qua Dez 26, 2012 21:22
Cálculo: Limites, Derivadas e Integrais
-
- Calculando a função através das coordenadas
por Fernanda Lauton » Dom Jun 13, 2010 20:36
- 2 Respostas
- 1626 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 14, 2010 16:06
Funções
-
- DETERMINAR FUNÇÃO ATRAVÉS DE COORDENADAS
por Fernanda Lauton » Qua Abr 06, 2011 14:41
- 1 Respostas
- 1730 Exibições
- Última mensagem por MarceloFantini

Qua Abr 06, 2011 19:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



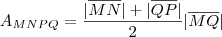
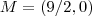 e
e  .
.  pertencentes ao gráfico
pertencentes ao gráfico 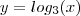 terão coordenadas ,
terão coordenadas , 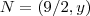 e
e  .
.  quando
quando 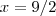 , basta resolver
, basta resolver  , para o outro ponto o processo é análogo .
, para o outro ponto o processo é análogo . 