inscrito no gráfico através de uma função... me ajudem.. eu só consigo
fazer uma coisa de cada vez... não sei literalmente por onde começar...
Postei a imagem do gráfico e a questão na internet... por favor me ajudem...
http://imageshack.us/photo/my-images/443/funo.jpg
Muito Obrigado;;; ;]
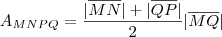
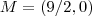e 
. 
pertencentes ao gráfico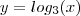 
terão coordenadas , 
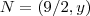e 
. 
quando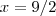 
, basta resolver 
, para o outro ponto o processo é análogo . 
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)