 por SCHOOLGIRL+T » Ter Nov 13, 2012 10:32
por SCHOOLGIRL+T » Ter Nov 13, 2012 10:32
A população de uma colonia de bactéria E.coli dobra a cada 20 mim . Em um experimento, colocou-se inicialmente em um tubo de ensaio uma amostra com 1000 bactérias por mililitro. No final do experimento obteve-se um total de
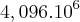
bactérias por mililitro. Assim sendo o tempo do experimento foi de?
Eu encontrei a resposta, 4 horas, fazendo como se fosse uma PG. Mas eu gostaria que vocês me ajudassem a fazer uma lei da função para esse exercício. Tipo, "a quantidade de bactérias por mililitro em função do tempo", porque eu não sei como se faz. Obrigada.
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Nov 13, 2012 16:22
por young_jedi » Ter Nov 13, 2012 16:22
como cresce expoencialmente então a equação é do tipo

como a população dobra a cada vinte minutos dividinto do tempo em minutos temos t/20

cmo no inicio (t=0) a população é 1000 então

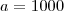
então a função sera

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por JU201015 » Ter Nov 13, 2012 19:48
por JU201015 » Ter Nov 13, 2012 19:48
young_jedi escreveu:como cresce expoencialmente então a equação é do tipo

como a população dobra a cada vinte minutos dividinto do tempo em minutos temos t/20

cmo no inicio (t=0) a população é 1000 então

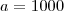
então a função sera

Ótima explicação! Obrigada^^
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1622 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2829 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2822 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2238 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2186 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
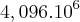 bactérias por mililitro. Assim sendo o tempo do experimento foi de?
bactérias por mililitro. Assim sendo o tempo do experimento foi de?




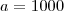



 .
.



