 por Lismara » Qua Set 16, 2009 22:18
por Lismara » Qua Set 16, 2009 22:18
Olá, preciso de ajuda para identificar o grau do polinômio [3ax³+5a²x²(x²+1)](3a³x²)(x³/ax²) na variável x
Já tentei várias vezes resolver, mas parece que não dá certo.Na minha resolução dá 7. Será que está correto?
As alternativas são:
a) 6
b) 4
c) 7
d)11
-
Lismara
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Ago 31, 2009 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por cristina » Qua Set 16, 2009 23:17
por cristina » Qua Set 16, 2009 23:17
Olá Lismara realmente estamos fazendo o meu curso que legal, adorei descubrir que tenho mais uma colega...
Olha eu consegui resolver este exercicio.... vou simplificar o resultado
![\left[3a{x}^{3} + 5{a}^{2}{x}^{2}+ 5 {a}^{2}{x}^{2} \right]\left(3{a}^{3}{x}^{2} \right)\left(\frac{{x}^{3}}{a{x}^{2}} \right) \left[3a{x}^{3} + 5{a}^{2}{x}^{2}+ 5 {a}^{2}{x}^{2} \right]\left(3{a}^{3}{x}^{2} \right)\left(\frac{{x}^{3}}{a{x}^{2}} \right)](/latexrender/pictures/dfc73a3c0a36811309d4400dfad20dea.png)

neste caso a resposta é 7...
Espero que tenha te ajudado....
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Lismara » Qua Set 16, 2009 23:38
por Lismara » Qua Set 16, 2009 23:38
Cristina, você já mandou este questionário para ver se esta questão está mesmo certa?
Porque alguns da minha cidade disseram que a resposta é 4, mas eu não consegui chegar a este resultado
-
Lismara
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Ago 31, 2009 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por cristina » Qua Set 16, 2009 23:49
por cristina » Qua Set 16, 2009 23:49
Lismara... eu já enviei todos os meus questionários, e consegui notas maxima...
Subtende-se que a questão esta certa...
E tbem eu peguei um livro de 8ª serie e tentei resolver.
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Lismara » Qui Set 17, 2009 00:05
por Lismara » Qui Set 17, 2009 00:05
Ok, obrigada, eu também cheguei ao resultado 7, mas precisava de uma confirmação.
-
Lismara
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Ago 31, 2009 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por cristina » Ter Set 22, 2009 12:08
por cristina » Ter Set 22, 2009 12:08
olá Lismara, td bem? vc esta conseguindo resolver os exercicios da fundamentos da matemática?
abraços
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por DanielFerreira » Ter Set 22, 2009 12:18
por DanielFerreira » Ter Set 22, 2009 12:18
Olá, preciso de ajuda para identificar o grau do polinômio [3ax³+5a²x²(x²+1)](3a³x²)(x³/ax²) na variável x
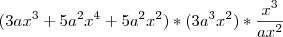
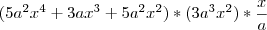

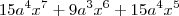
logo,
gab. "
c"
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Lismara » Ter Set 22, 2009 20:55
por Lismara » Ter Set 22, 2009 20:55
Olá Cristina, estamos tentando , mas essa disciplina parece mais difícil que as outras, mas se Deus quiser vamos conseguir. E você tá conseguindo?
-
Lismara
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Ago 31, 2009 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por cristina » Qua Set 23, 2009 00:05
por cristina » Qua Set 23, 2009 00:05
Olá
Tbem estou encontrando grandes dificuldades....
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8361 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
-
- Polinômios de grau 4
por Florisbela » Dom Mai 23, 2010 19:22
- 3 Respostas
- 2784 Exibições
- Última mensagem por MarceloFantini

Seg Mai 24, 2010 21:35
Polinômios
-
- raizes de polinomios de grau 3
por theSinister » Seg Mai 09, 2011 17:58
- 9 Respostas
- 5472 Exibições
- Última mensagem por theSinister

Seg Mai 09, 2011 21:35
Álgebra Elementar
-
- Simplificação do quociante de polinômios de quarto grau
por Caroline Oliveyra » Qui Jun 23, 2011 22:19
- 4 Respostas
- 4011 Exibições
- Última mensagem por Caroline Oliveyra

Qui Jun 23, 2011 23:36
Polinômios
-
- Equações de 1 grau e 2 grau
por Neperiano » Sex Out 10, 2008 22:22
- 7 Respostas
- 13976 Exibições
- Última mensagem por DanielFerreira

Dom Jul 26, 2009 12:55
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\left[3a{x}^{3} + 5{a}^{2}{x}^{2}+ 5 {a}^{2}{x}^{2} \right]\left(3{a}^{3}{x}^{2} \right)\left(\frac{{x}^{3}}{a{x}^{2}} \right) \left[3a{x}^{3} + 5{a}^{2}{x}^{2}+ 5 {a}^{2}{x}^{2} \right]\left(3{a}^{3}{x}^{2} \right)\left(\frac{{x}^{3}}{a{x}^{2}} \right)](/latexrender/pictures/dfc73a3c0a36811309d4400dfad20dea.png)


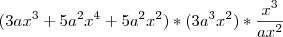
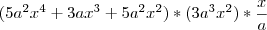

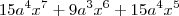

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.