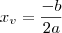[Função Quadrática] Me ajudem

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Função Quadrática] Me ajudem

Regras do fórum
Responder

[Função Quadrática] Me ajudem

Mensagempor thayna_rosa » Seg Nov 12, 2012 18:46

Determine as coordenadas do vértice da parábola que representa a função: g(x)=-3(x-4)²+2
thayna_rosa
Novo Usuário
Novo Usuário
 
Mensagens: 5
Registrado em: Seg Nov 12, 2012 18:28
Formação Escolar: ENSINO FUNDAMENTAL II
Andamento: cursando
Voltar ao topo

Re: [Função Quadrática] Me ajudem

Mensagempor thayna_rosa » Seg Nov 12, 2012 20:01

não sei o que fazer depois que resolvo o produto notável
thayna_rosa
Novo Usuário
Novo Usuário
 
Mensagens: 5
Registrado em: Seg Nov 12, 2012 18:28
Formação Escolar: ENSINO FUNDAMENTAL II
Andamento: cursando
Voltar ao topo

Re: [Função Quadrática] Me ajudem

Mensagempor MarceloFantini » Seg Nov 12, 2012 20:47

Existem duas formas de responder: uma é lembrar que a abscissa do vértice é dada por x_v = \frac{-b}{2a}, substituir na fórmula e encontrar a ordenada y_v correspondente.

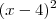Outra forma, mais interessante, é perceber que (x-4)^2 sempre será maior ou igual a zero, pois é um número ao quadrado. Daí temos que 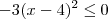-3(x-4)^2 \leq 0 pelas propriedades de desigualdade. Somando-se dois de ambos lados segue que 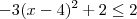-3(x-4)^2 +2 \leq 2. Isto acontece se e somente se x=4, que é a condição para que -3(x-4)^2 =0.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo
Responder

Voltar para Funções

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

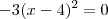Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum