1.2) - E agora, no meio do percurso, senti a necessidade de fazer uma revisão sobre trigonometria - conteúdo este que não sou lá estas coisas - e eis que me deparo com um entrave. Não consigo entender a seção "Relações entre comprimento de arco, ângulo, raio e área" do apêndice "Revisão de Trigonometria", páginas: A2 e A3. Primeiramente, gostaria de descrever a situação exposta no livro e em seguida, faço minhas observações e digo o que não entendi, no final.
1.3) - O autor inicia a sessão explanando sobre uma relação da geometria plana que afirma:
"Para dois círculos concêntricos, a razão entre os comprimentos de arco subentendidos por um ângulo central é igual à razão dos raios correspondentes." (O que obviamente permite concluir que:)

fórmula-1:
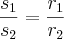
1.4) - Em seguida afirma que:
"Em particular, se 's' for o comprimento de arco subentendido sobre um círculo de raio 'r' por um ângulo '?' radianos, então, comparando com o comprimento de arco subentendido pelo mesmo ângulo sobre um círculo de raio igual a 1(um), obtemos:"

fórmula-2:
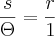
1.5) - Ele observa na lateral da página que:
"Se ? estiver em radianos, então:"
fórmula-3:
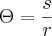
Dúvida:
1) - Eu simplesmente não consigo entender como o sujeito chega a fórmula-2 e muito menos a fórmula-3
2) - Ele fala em comparação ("[..]comparando com o comprimento de arco[..]", citação de 1.4 ): o que exatamente seria esta comparação? Ele está lançando uma igualdade? Não entendi exatamente como transcrevo matematicamente o que ele disse.
PS: Se talvez a dúvida seja idiota ou algo que o valha, por favor, deixem uma referência de algum site ou material que tenha explicação sobre o assunto.
Obrigado pela atenção.
Abraços.
Att. Matheus L. Oliveira.





