 por Crist » Dom Nov 11, 2012 16:40
por Crist » Dom Nov 11, 2012 16:40
Preciso resolver esta integral pelo metodo da substituição , mas não consigo chegar na igualdade dada.
![\int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2 \int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2](/latexrender/pictures/8266ac2f4250d2c56428b4c9ca2e8e86.png)

[tex]2/6 \left( (1 +x^2 \right)^3/2 + c
fiz as devidas contas e substituições mas não consigo chegar nesse resultado, será que alguém pode me ajudar?
espero que entendam, pois ainda estou aprendendo a usar o latex
-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Nov 11, 2012 17:27
por e8group » Dom Nov 11, 2012 17:27
Acredito que você fez foi isto ,
i) Fazendo ,

ii) Daí ,
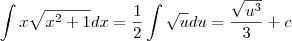
iii) Voltando para variavel

, temos
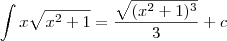
iv) Conclusão ,

Veja os códigos usados
i)
- Código: Selecionar todos
x^2 + 1 \implies du = 2x dx
ii)
- Código: Selecionar todos
\int x\sqrt{x^2 +1} dx = \frac{1}{2}\int \sqrt{u} du = \frac{ \sqrt{u^3} } {3} + c
iii)
- Código: Selecionar todos
\int x\sqrt{x^2 +1} = \frac{ \sqrt{(x^2 + 1)^3} } {3} + c
iv)
- Código: Selecionar todos
\int_{0} ^5 x\sqrt{x^2 +1} dx = \frac{\sqrt{(5^2 +1)^3} - 1}{3} = \frac{26 \sqrt{26} - 1}{3} \neq 921,342
Cada código foi inserindo dentro de [ tex ] ....... [ / tex ] . ( sem espaço como estar escrito )
Realmente não consegui chegar no resultado , talvez há um erro de digitação . Por favor conferi o mesmo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Crist » Dom Nov 11, 2012 19:26
por Crist » Dom Nov 11, 2012 19:26
Não há erro de digitação, refiz novamente e não chego ao resultado, vou ver com minha professora deve ter um erro na questão, muito obrigada pela ajuda.
-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Crist » Seg Nov 12, 2012 21:15
por Crist » Seg Nov 12, 2012 21:15
realmente o professor errou na hora de postar o resultado, na verdade é 43,86
-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3675 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3065 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2498 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3624 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2 \int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2](/latexrender/pictures/8266ac2f4250d2c56428b4c9ca2e8e86.png)
 [tex]2/6 \left( (1 +x^2 \right)^3/2 + c
[tex]2/6 \left( (1 +x^2 \right)^3/2 + c
![\int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2 \int_{0}^{5}x\sqrt[2]{1+x^2}dx = 921,342
[tex]u= 1+x^2](/latexrender/pictures/8266ac2f4250d2c56428b4c9ca2e8e86.png)
 [tex]2/6 \left( (1 +x^2 \right)^3/2 + c
[tex]2/6 \left( (1 +x^2 \right)^3/2 + c

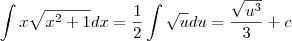
 , temos
, temos 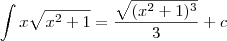




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.