ax+bx+ay+by=
x(a+b)+y(a+b)=
(a+b)(x+y)
---------------------------------------------
mx-nx+2m-2n=
x(m-n)+2(m-n)=
(m-n).(x+2)
--------------------------------------------
a³+a²+a+1=
a².(a+1)+1.(a+1)=
(a+1).(a²+1)
-----------------------------------------------
2ax+bx-10a-5b=
x(2a+b)-5(2a+b)=
(2a+b).(x-5)
-------------------------
3ax+6a+b²x+2b²=
3a(x+2)+b²(x+2)=
(x+2).(3a+b²)
....................................................
Eu só queria uma explicação para saber como se chega a esse resultado, pode ser com ouro exemplos rsrs
recebi ajuda de outro professor aki do ajuda matemática , mas eu estava lendo a sua resposta e ela me ajudou muito, mas eu resolvi postar outra só por precaução rsrs



 , então vamos colocá-lo em
, então vamos colocá-lo em  .
.
 é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:
é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:![\\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)} \\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)}](/latexrender/pictures/ac83ee463b71cde006899cad281d12f1.png)


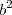

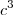

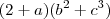

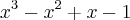
 porque ele é o maior divisor dos dois primeiros elementos simultaneamente.
porque ele é o maior divisor dos dois primeiros elementos simultaneamente.




