 por Estudante13 » Sex Nov 09, 2012 23:30
por Estudante13 » Sex Nov 09, 2012 23:30
TITULO: Fatoração por agrupamento
ax+bx+ay+by=
x(a+b)+y(a+b)=
(a+b)(x+y)
---------------------------------------------
mx-nx+2m-2n=
x(m-n)+2(m-n)=
(m-n).(x+2)
--------------------------------------------
a³+a²+a+1=
a².(a+1)+1.(a+1)=
(a+1).(a²+1)
-----------------------------------------------
2ax+bx-10a-5b=
x(2a+b)-5(2a+b)=
(2a+b).(x-5)
-------------------------
3ax+6a+b²x+2b²=
3a(x+2)+b²(x+2)=
(x+2).(3a+b²)
....................................................
Eu só queria uma explicação para saber como se chega a esse resultado, pode ser com ouro exemplos rsrs
recebi ajuda de outro professor aki do ajuda matemática , mas eu estava lendo a sua resposta e ela me ajudou muito, mas eu resolvi postar outra só por precaução rsrs

Obrigada pela atenção.
Estudante13
-
Estudante13
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 04, 2012 15:40
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Nenhum
- Andamento: cursando
 por DanielFerreira » Sex Nov 09, 2012 23:55
por DanielFerreira » Sex Nov 09, 2012 23:55
Estudante13,
acredito que você tenha se referido ao
Cleyson007, né? Então, se você entendeu direitinho o que ele te explicou vai ficar mais fácil compreender o
agrupamento.
O
fator comum aos dois primeiros termos é o

, então vamos colocá-lo em
evidência; faça o mesmo com o 3º e o 4º termo, nesse caso, o fator comum é o

.

Note que

é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:
![\\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)} \\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)}](/latexrender/pictures/ac83ee463b71cde006899cad281d12f1.png)
Siga o mesmo raciocínio para os outros exemplos.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Estudante13 » Sáb Nov 10, 2012 20:00
por Estudante13 » Sáb Nov 10, 2012 20:00
danjr5 escreveu:Estudante13,
acredito que você tenha se referido ao
Cleyson007, né? Então, se você entendeu direitinho o que ele te explicou vai ficar mais fácil compreender o
agrupamento.
O
fator comum aos dois primeiros termos é o

, então vamos colocá-lo em
evidência; faça o mesmo com o 3º e o 4º termo, nesse caso, o fator comum é o

.

Note que

é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:
![\\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)} \\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)}](/latexrender/pictures/ac83ee463b71cde006899cad281d12f1.png)
Siga o mesmo raciocínio para os outros exemplos.
Ok, mas eu... sei la não to conseguindo entender fatoração de agrupamento, eu tava fazendo um exercício e não entendi o fator comum dele...
x³-x²+x-1=
x²(x-1)+1.(x-1)-------------- Porque o fator comum é "x²" porque??
(x-1).(x²+1)
--------------------------------------------------------------------------------------
outra pergunta rsrs,
nunca consigo chegar ao resultado final dessas 2 contas rsrs, de todas as contas desse tipo rsrsr
a) xy-y+rs-s=
b)2b²+ab²+2c³+ac3
c) 4y? - 6y? +8y -12=
...Por exemplo,
a letra:
c) 4y? - 6y? +8y -12=
2(y-3/2)(2y?+4)= ------------Pq o fator comum é 2? e uma explicação para chegar ao resultado
2(y-3/2)(y?+2)
b)2b²+ab²+2c³+ac3
b(2+a+b)+c(2+c)
o meu resultado dessa conta foi= (b+c)(2+a+b+c)---- sei que está errado o resultado mas não consigo botar o correto uma explicação pf pf pf ( sei que estou abusando aqui do ajuda matemática mas porfavor rsrs)
Obrigada pela atenção.
Estudante13
-
Estudante13
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 04, 2012 15:40
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Nenhum
- Andamento: cursando
 por young_jedi » Sáb Nov 10, 2012 21:04
por young_jedi » Sáb Nov 10, 2012 21:04

nos dois primeiros termos da expressão temos que o elemento em comum neles é
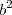
colocando em evidencia

nos dois ultimos termos temos que o elemento comum deles é
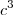
colocando em evidencia

temos agora uma expressão que é a soma de dois termos, e o elemento em comum entre eles é o (2+a) então colocando em evidencia
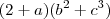
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Cleyson007 » Sáb Nov 10, 2012 21:09
por Cleyson007 » Sáb Nov 10, 2012 21:09
Olá, boa noite!
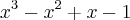
Foi escolhido o

porque ele é o maior divisor dos dois primeiros elementos simultaneamente.
Quanto ao terceiro e quarto elemento foi multiplicado por 1.
Quanto às outras dúvidas:
a)

Analisando os dois primeiros elementos (que tem elementos em comum y)..

Analisando o terceiro e o quarto elemento (que tem elementos em comum s)..

Resultado:

A segunda dúvida o Young_jedi já te ajudou

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3254 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [Fatoração] Agrupamento.
por replay » Qui Dez 13, 2012 17:05
- 3 Respostas
- 2682 Exibições
- Última mensagem por DanielFerreira

Sex Dez 28, 2012 22:09
Álgebra Elementar
-
- Agrupamento, centroid e intervalos
por fjucks » Sex Jan 06, 2012 18:58
- 1 Respostas
- 1456 Exibições
- Última mensagem por fjucks

Sáb Jan 07, 2012 14:26
Álgebra Elementar
-
- analise combinatoria, agrupamento
por zenildo » Sáb Ago 31, 2013 00:55
- 1 Respostas
- 1576 Exibições
- Última mensagem por paulo testoni

Sex Out 18, 2013 18:43
Análise Combinatória
-
- analise combinatoria, agrupamento
por zenildo » Sáb Ago 31, 2013 00:58
- 1 Respostas
- 2246 Exibições
- Última mensagem por matano2104

Qui Set 19, 2013 15:24
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , então vamos colocá-lo em
, então vamos colocá-lo em  .
.
 é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:
é o fator comum do "1º" e "2º" termos, portanto, podemos colocá-lo em evidência, veja:![\\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)} \\ (a + b)[x + y] = \\\\ \boxed{(a + b)(x + y)}](/latexrender/pictures/ac83ee463b71cde006899cad281d12f1.png)


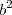

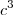

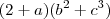

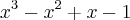
 porque ele é o maior divisor dos dois primeiros elementos simultaneamente.
porque ele é o maior divisor dos dois primeiros elementos simultaneamente.




