 por Danilo Dias Vilela » Ter Set 15, 2009 21:45
por Danilo Dias Vilela » Ter Set 15, 2009 21:45
Pessoal me ajude no seguinte exercício: 3. Todos os candidatos inscritos num vestibular escolheram na ficha de inscrição que preencheram uma única entre as três seguintes situações prévias (em relação ao ano anterior): freqüentou um cursinho, acabou de sair do ensino médio ou estudou sozinho. Por um erro no processamento dos dados, foi gerado um relatório sobre essas respostas apenas com as seguintes informações :
I. 800 não fizeram cursinho,
II. 1200 não acabaram de sair do ensino médio,
III. 1500 não ficaram estudando sozinhos durante o último ano.
Qual é o número total de inscritos?
Minha Resolução:
Fizeram cursinho Sim: x Não: 800
Acabaram de sair do ensino médio Sim: y Não: 1200
Ficaram estudando sozinhos durante o último Sim: z Não: 1500
Como montar as equações é que não sei. Por favor alguém me ajude somente à montar às equações. O resto eu faço. Obrigado
-
Danilo Dias Vilela
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Set 09, 2009 01:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Molina » Qua Set 16, 2009 00:25
por Molina » Qua Set 16, 2009 00:25
Boa noite, Danilo.
Você pode pensar assim e reescrever os itens I, II e III:
I. 800 não fizeram cursinho,
Se 800 não fizeram cursinho é porque 800 ou fizeram ensino médio ou estudaram sozinhoII. 1200 não acabaram de sair do ensino médio,
Se 1200 não fizeram ensino médio é porque 1220 ou fizeram cursinho ou estudaram sozinhoIII. 1500 não ficaram estudando sozinhos durante o último ano.
Se 1500 não estudaram sozinhi é porque 1500 ou fizeram ensino médio ou fizeram cursinhoChame cada uma das possibilidades de X, Y, Z.
X = Ensino Médio
Y = Sozinho
Z = Cursinho
Pelo item I) temos que:
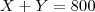
Faça o item II e o item III. Com isso você vai obter outras duas equações.
Logo, temos 3 equações com 3 incognitas.
Basta substituir uma na outra e encontrar o valor que você deseja.
Qualquer dúvida manda ae,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Danilo Dias Vilela » Qua Set 16, 2009 11:50
por Danilo Dias Vilela » Qua Set 16, 2009 11:50
Valeu pela ajuda Molina! Achei x=550; y=250 e z=950, sendo o total de inscritos x+y+z=550+250+950=1750. É uma questão de interpretação também. Valeu!!!

-
Danilo Dias Vilela
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Set 09, 2009 01:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2663 Exibições
- Última mensagem por admin

Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1274 Exibições
- Última mensagem por Molina

Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1436 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
- 1 Respostas
- 2300 Exibições
- Última mensagem por Molina

Qui Set 10, 2009 14:15
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 00:25
- 2 Respostas
- 2267 Exibições
- Última mensagem por RICI

Sex Ago 24, 2012 11:58
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


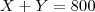


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.